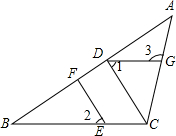
如图.在△ABC中.DG∥BC.∠1=∠2．(1)试说明EF∥DC,(2)如果CD⊥AB.∠B=36°.∠ACD=50°.求∠3度数．题目和参考答案——青夏教育精英家教网—

11．

如图，在△ABC中，DG∥BC，∠1=∠2．
（1）试说明EF∥DC；
（2）如果CD⊥AB，∠B=36°，∠ACD=50°，求∠3度数．

分析（1）欲证明EF∥DC，只要证明∠2=∠DCB即可．
（2）求出∠ACB，根据DG∥BC，可得∠3=∠ACB；

解答解：（1）∵DG∥BC，
∴∠1=∠DCB，
∵∠1=∠2，
∴∠DCB=∠2，
∴EF∥DC（内错角相等，两直线平行）．

（2）∵CD⊥AB，
∴∠BDC=90°，
∵∠B=36°，
∴∠BCD=90°-36°=54°，
∵∠ACD=50°，
∴∠ACB=54°+50°=104°，
∵DG∥BC，
∴∠3=∠ACB=104°．

点评本题考查三角形内角和定理、平行线的性质、垂线的性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考基础题．

练习册系列答案

优加学案中考真题详解汇编系列答案

同行课课100分过关作业系列答案

举一反三全能训练系列答案

快乐的假期生活寒假作业哈尔滨出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

4．某地区为了进一步缓解交通拥堵问题，决定修建一条长为6千米的公路．如果平均每天的修建费y（万元）与修建天数x（天）之间在50≤x≤120时，具有一次函数的关系，如表所示．

x	50	80	100	120
y	40	34	30	26

（1）求y关于x的函数解析式；
（2）如果修建70天，那么平均每天的修建费是多少？

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

2．

某校组织1000名学生参加“青少年普法知识大赛”，为了了解学生的参赛成绩，从中抽取部分学生的参赛成绩（成绩均为整数）进行统计，并绘制成如下的不完全统计图表．

组别	分数段	频数	频率
一	50.5-60.5	16	0.08
二	60.5-70.5	30	0.15
三	70.5-80.5	50	0.25
四	80.5-90.5	m	0.40
五	90.5-100.5	24	n

请根据所给信息，解答下列问题：
（1）表中m=80，n=0.12；
（2）补全频数分布直方图；
（3）若成绩超过80分为优秀，分别求出被抽取的学生中优秀的学生频数和频率．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

19．感知：如图①，AD平分∠BAC，∠B+∠C=180°，∠B=90°，易知：DB=DC．
探究：如图②，在四边形ABDC中，AD平分∠BAC，∠B=45°，∠C=135°，试说明：DB与DC的数量关系，并说明原因．
应用：如图③，在四边形ABDC中，AD平分∠BAC，∠ABD+∠ACD=180°，∠ABD＜90°，DB与DC的上述关系还成立吗？并说明原因．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

6．

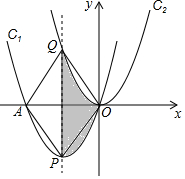如图，在平面直角坐标系xOy中，抛物线C₁的顶点为P（-3，-$\frac{9}{2}$），且过点O（0，0）．
（1）写出抛物线C₁与x轴的另一个交点A的坐标；
（2）将抛物线C₁向右平移3个单位、再向上平移4.5个单位得抛物线C₂，求抛物线C₂的解析式；
（3）直接写出阴影部分的面积S．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

16．

如图，平面直角坐标系中，已知A（-3，1）、B（0，3）、C（-4，3）．
（1）将△ABC经过平移后得到△A₁B₁C₁，若点C₁的坐标为（0，-1），在图中画出△A₁B₁C₁；
（2）顶点A₁坐标为（1，-3），B₁的坐标为（4，-1）；
（3）将△ABC绕点P沿顺时针方向旋转后得到△A₂B₂C₂，则点P的坐标是（0，-1），旋转角的度数是90°．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

3．已知正比例函数y=（k-2）x的图象经过第一、三象限，则k的值可能是（　　）

A．

-2

B．

C．

D．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

20．在$\sqrt{\frac{49}{100}}$，$\frac{1}{π}$，$\sqrt{7}$，$\frac{101}{11}$，0.10111213…中，无理数的个数是（　　）

A．