
ЎҫМвДҝЎҝРЎГч°пЦъРЎ·јөҙЗпЗ§ЈЁИзНј1Ј©Ј¬ФЪРЎГчөДЦъНЖПВЈ¬ЗпЗ§ФҪАҙФҪёЯЈ¬ЗпЗ§АлөШГжөДёЯ¶И![]() ЈЁ
ЈЁ![]() Ј©Ул°Ъ¶ҜКұјд
Ј©Ул°Ъ¶ҜКұјд![]() ЈЁ
ЈЁ![]() Ј©Ц®јдөД№ШПөИзНј2ЛщКҫ.
Ј©Ц®јдөД№ШПөИзНј2ЛщКҫ.
ЈЁ1Ј©ёщҫЭәҜКэ¶ЁТеЈ¬ЗлЕР¶ПұдБҝ![]() КЗ·сОӘ№ШУЪ
КЗ·сОӘ№ШУЪ![]() өДәҜКэЈҝ
өДәҜКэЈҝ
ЈЁ2Ј©ҪбәПНјПу»ШҙрЈә
ўЩЗпЗ§ҫІЦ№КұАлөШГжөДҫаАлКЗ¶аЙЩЈҝЗпЗ§өДЧоёЯөгУлөШГжҫаАлКЗ¶аЙЩЈҝ
ўЪ¶аіӨКұјдәуРЎГчҫНІ»ФЩНЖРЎ·јЈҝ
ўЫҙУЧоөНөгҝӘКјПтЗ°әНПтәуЈ¬ФЩ·ҙ»ЪөҪЧоөНөгЈ¬ХвҪРЧцТ»ёцЦЬЖЪЈ¬ЗлОКЈ¬РЎ·јНкіЙөЪТ»ёцЦЬЖЪУГБЛ¶аіӨКұјдЈҝ
ўЬГҝёцЦЬЖЪөДКұјд¶јКЗПаөИөДЈ¬ҫӯ№э¶аіӨКұјдЈ¬ЗпЗ§өДЧоёЯөгКЗ1mЈҝ

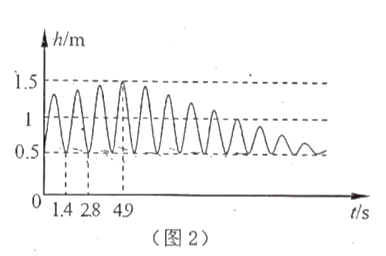
Ўҫҙр°ёЎҝЈЁ1Ј©КЗЈ»ЈЁ2Ј©ўЩ0.5mЈ¬1.5mЈ»ўЪ4.9sЈ»ўЫ2.8sЈ»ўЬ11.9s
ЎҫҪвОцЎҝ
ЈЁ1Ј©ёщҫЭәҜКэөД¶ЁТеЈә¶ФУЪГҝТ»ёцИ·¶ЁөДxЦөЈ¬¶јУРОЁТ»өДyЦөУлЖд¶ФУҰ.ҪбәПНјПујҙҝЙҪвҙрЈ»
ЈЁ2Ј©ўЩёщҫЭәҜКэНјПуЈ¬ЧоөНөгјҙОӘЗпЗ§ҫІЦ№КұУлөШГжөДҫаАлЈ¬ЧоёЯөгУлөШГжөДҫаАл№ЫІмНјПуҝЙЦӘЈ»
ўЪРЎГчІ»ФЩНЖРЎ·јҝӘКјЈ¬РЎ·јҫаАлөШГжөДЧоёЯөгҝӘКјВэВэұдРЎЈ¬ҪбәПНјПуҝЙЦӘКұјдЈ»
ўЫёщҫЭМвДҝМхјюёшіцөДЦЬЖЪөД¶ЁТеҝЙЦӘЈәЧоөНөгЎъПтЗ°ЧоёЯөгЎъЧоөНөгЎъПтәуЧоёЯөгЎъЧоөНөгОӘТ»ёцЦЬЖЪЈ¬ҪбәПНјПуҝЙЦӘТ»ёцЦЬЖЪөДКұјдЈ»
ўЬПИёщҫЭНјПуХТөҪЗпЗ§өДЧоёЯөгКЗ1mөДөгөДО»ЦГЈ¬И»әуҝҙТ»ПВУР¶аЙЩёцЦЬЖЪЈ¬іЛТФЦЬЖЪөДКұјдјҙҝЙ.
ЈЁ1Ј©ұдБҝ![]() КЗ·сОӘ№ШУЪ
КЗ·сОӘ№ШУЪ![]() өДәҜКэ.УЙНјПуҝЙЦӘЈ¬¶ФУЪГҝТ»ёц°Ъ¶ҜКұјдtЈ¬h¶јУРОЁТ»И·¶ЁөДЦөУлЖд¶ФУҰЈ¬ЛщТФұдБҝhКЗ№ШУЪtөДәҜКэЈ»
өДәҜКэ.УЙНјПуҝЙЦӘЈ¬¶ФУЪГҝТ»ёц°Ъ¶ҜКұјдtЈ¬h¶јУРОЁТ»И·¶ЁөДЦөУлЖд¶ФУҰЈ¬ЛщТФұдБҝhКЗ№ШУЪtөДәҜКэЈ»
ЈЁ2Ј©ўЩУЙНјПуҝЙЦӘЈ¬ЧоөНөгҫНКЗЗпЗ§ҫІЦ№КұУлөШГжөДҫаАлЈ¬ЛщТФЗпЗ§ҫІЦ№КұАлөШГжөДҫаАлКЗ0.5mЈ¬ЗпЗ§өДЧоёЯөгУлөШГжҫаАлКЗ1.5mЈ»
ўЪУЙНјПуҝЙЦӘЈ¬ҙУ4.9sҝӘКјЈ¬ЗпЗ§өДЧоёЯөгУлөШГжҫаАлВэВэұдРЎЈ¬ЛщТФ4.9sәуЈ¬РЎГчҫНІ»ФЩЦъНЖРЎ·јЈ»
ўЫУЙМвТвҝЙЦӘЦЬЖЪөД¶ЁТеЈ¬ёщҫЭНјПуҝЙЦӘЈ¬РЎ·јНкіЙөЪТ»ёцЦЬЖЪУГБЛ2.8sЈ»
ўЬУЙНјПуҝЙЦӘЈ¬ЗпЗ§өДЧоёЯөгКЗ1mКұЈ¬ҫӯ№эБЛ![]() ёцЦЬЖЪЈ¬¶шТ»ёцЦЬЖЪОӘ2.8sЈ¬ЛщТФЗпЗ§өДЧоёЯөгКЗ1mКұЈ¬ЛщУГКұјдОӘЈә
ёцЦЬЖЪЈ¬¶шТ»ёцЦЬЖЪОӘ2.8sЈ¬ЛщТФЗпЗ§өДЧоёЯөгКЗ1mКұЈ¬ЛщУГКұјдОӘЈә![]() ,№Кҫӯ№э11.9sЗпЗ§өДЧоёЯөгКЗ1m.
,№Кҫӯ№э11.9sЗпЗ§өДЧоёЯөгКЗ1m.


 Т»ПЯГыКҰМбУЕКФҫнПөБРҙр°ё
Т»ПЯГыКҰМбУЕКФҫнПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪДіРЈЧйЦҜөДіхЦРКэС§УҰУГДЬБҰҫәИьЦРЈ¬Гҝ°аІОјУұИИьөДИЛКэПаН¬Ј¬іЙјЁ·ЦОӘAЎўBЎўCЎўDЛДёцөИј¶Ј¬ЖдЦРПаУҰөИј¶өДөГ·ЦТАҙОјЗОӘ100·ЦЎў90·ЦЎў80·ЦЎў70·ЦЈ¬С§РЈҪ«°ЛДкј¶өДТ»°аәН¶ю°аөДіЙјЁХыАнІў»жЦЖіЙИзПВөДНіјЖНјЈ¬¶ю°аDј¶№ІУР4ИЛЈ®

ЗлДгёщҫЭТФЙПМṩөДРЕПўҪвҙрПВБРОКМвЈә
ЈЁ1Ј©ЗуҙЛҫәИьЦРТ»°а№ІУР¶аЙЩИЛІОјУұИИьЈ¬ІўІ№И«МхРОНіјЖНјЈ®
ЈЁ2Ј©ЙИРОНіјЖНјЦРAј¶¶ФУҰөДФІРДҪЗ¶ИКэКЗЎЎ ЎЎЈ®
ЈЁ3Ј©ҙЛҙОҫәИьЦР¶ю°аФЪCј¶ТФЙПЈЁ°ьАЁCј¶Ј©өДИЛКэОӘЎЎ ЎЎЈ®
ЈЁ4Ј©ЗлДгҪ«ұнёсІ№ідНкіЙЈә

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТ»ГыЧгЗтКШГЕФұБ·П°ХЫ·өЕЬЈ¬ҙУЗтГЕПЯіц·ўЈ¬ПтЗ°јЗЧчХэКэЈ¬·ө»ШјЗЧчёәКэЈ¬ЛыөДјЗВјИзПВЈәЈЁөҘО»ЈәГЧЈ©+5Ј¬-3Ј¬+10Ј¬-8Ј¬-6Ј¬+12Ј¬-10
ЈЁ1Ј©КШГЕФұЧоәуКЗ·с»ШөҪБЛЗтГЕПЯөДО»ЦГЈҝ
ЈЁ2Ј©ФЪБ·П°№эіМЦРЈ¬КШГЕФұАлҝӘЗтГЕЧоФ¶ҫаАлКЗ¶аЙЩГЧЈҝ
ЈЁ3Ј©КШГЕФұИ«ІҝБ·П°ҪбКшәуЈ¬Лы№ІЕЬБЛ¶аЙЩГЧЈҝ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ТСЦӘ![]() Ј¬ЙдПЯ
Ј¬ЙдПЯ![]() ҙУ
ҙУ![]() өДО»ЦГҝӘКјИЖөг
өДО»ЦГҝӘКјИЖөг![]() °ҙЛіКұХл·ҪПтРэЧӘЈ¬ЛЩ¶ИКЗГҝГл
°ҙЛіКұХл·ҪПтРэЧӘЈ¬ЛЩ¶ИКЗГҝГл![]() Ј¬Н¬КұЙдПЯ
Ј¬Н¬КұЙдПЯ![]() ҙУ
ҙУ![]() өДО»ЦГҝӘКјИЖөг
өДО»ЦГҝӘКјИЖөг![]() °ҙДжКұХл·ҪПтРэЧӘЈ¬ЛЩ¶ИКЗГҝГл
°ҙДжКұХл·ҪПтРэЧӘЈ¬ЛЩ¶ИКЗГҝГл![]() Ј¬ЙиРэЧӘКұјдОӘ
Ј¬ЙиРэЧӘКұјдОӘ![]() Гл
Гл![]() .
.
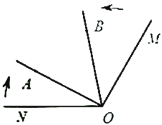
ЈЁ1Ј©УГә¬![]() өДҙъКэКҪұнКҫ
өДҙъКэКҪұнКҫ![]() әН
әН![]() өД¶ИКэЈ»
өД¶ИКэЈ»
ЈЁ2Ј©ФЪРэЧӘ№эіМЦРЈ¬өұ![]() өИУЪ
өИУЪ![]() КұЈ¬Зу
КұЈ¬Зу![]() өДЦөЈ»
өДЦөЈ»
ЈЁ3Ј©ФЪРэЧӘ№эіМЦРКЗ·сҙжФЪХвСщөД![]() Ј¬К№өГЙдПЯ
Ј¬К№өГЙдПЯ![]() ЗЎәГКЗНјЦРДіёцҪЗөДЖҪ·ЦПЯЈҝИз№ыҙжФЪЈ¬ЗлЗуіц
ЗЎәГКЗНјЦРДіёцҪЗөДЖҪ·ЦПЯЈҝИз№ыҙжФЪЈ¬ЗлЗуіц![]() өДЦөЈ»Из№ыІ»ҙжФЪЈ¬ЗлЛөГчАнУЙ.
өДЦөЈ»Из№ыІ»ҙжФЪЈ¬ЗлЛөГчАнУЙ.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘaЈ¬bОӘКөКэЈ¬ПВБРЛө·ЁЈәўЩИфaЈ¬b»ҘОӘПа·ҙКэЈ¬Фт![]() ЈҪ©Ғ1Ј»ўЪИфa+bЈј0Ј¬abЈҫ0Ј¬Фт|2a+b|ЈҪ©Ғ2a©ҒbЈ»ўЫИф|a|Јҫ|b|Ј¬ФтЈЁa+bЈ©ЈЁa©ҒbЈ©КЗХэКэЈ»ЖдЦРХэИ·өДУРЈЁЎЎЎЎЈ©ёцЈ®
ЈҪ©Ғ1Ј»ўЪИфa+bЈј0Ј¬abЈҫ0Ј¬Фт|2a+b|ЈҪ©Ғ2a©ҒbЈ»ўЫИф|a|Јҫ|b|Ј¬ФтЈЁa+bЈ©ЈЁa©ҒbЈ©КЗХэКэЈ»ЖдЦРХэИ·өДУРЈЁЎЎЎЎЈ©ёцЈ®
A.0B.1C.2D.3
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘЈәИзНјЈ¬ТСЦӘЦұПЯABөДәҜКэҪвОцКҪОӘy=©Ғ2x+8Ј¬УлxЦбҪ»УЪөгAЈ¬УлyЦбҪ»УЪөгBЈ®
ЈЁ1Ј©ЗуAЎўBБҪөгөДЧшұкЈ»
ЈЁ2Ј©ИфөгPЈЁmЈ¬nЈ©ОӘПЯ¶ОABЙПөДТ»ёц¶ҜөгЈЁУлAЎўBІ»ЦШәПЈ©Ј¬ЧчPEЎНxЦбУЪөгEЈ¬PFЎНyЦбУЪөгFЈ¬Б¬ҪУEFЈ¬ОКЈә
ўЩИфЎчPAOөДГж»эОӘSЈ¬ЗуS№ШУЪmөДәҜКэ№ШПөКҪЈ¬ІўРҙіцmөДИЎЦө·¶О§Ј»
ўЪКЗ·сҙжФЪөгPЈ¬К№EFөДЦөЧоРЎЈҝИфҙжФЪЈ¬ЗуіцEFөДЧоРЎЦөЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ»ҜјтЗуЦөЈә
ЈЁ1Ј©өұa=©Ғ1Ј¬b=2КұЈ¬ЗуҙъКэКҪ©Ғ2ЈЁab©Ғ3b2Ј©©Ғ[6b2©ҒЈЁab©Ғa2Ј©]өДЦө
ЈЁ2Ј©ПИ»ҜјтЈ¬ФЩЗуЦөЈә4xy©Ғ2ЈЁ![]() x2©Ғ3xy+2y2Ј©+3ЈЁx2©Ғ2xyЈ©Ј¬өұЈЁx©Ғ3Ј©2+|y+1|=0Ј¬ЗуКҪЧУөДЦө
x2©Ғ3xy+2y2Ј©+3ЈЁx2©Ғ2xyЈ©Ј¬өұЈЁx©Ғ3Ј©2+|y+1|=0Ј¬ЗуКҪЧУөДЦө
ЈЁ3Ј©ИфЈЁ2mx2©Ғx+3Ј©©ҒЈЁ3x2©Ғx©Ғ4Ј©өДҪб№ыУлxөДИЎЦөОЮ№ШЈ¬ЗуmөДЦө
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
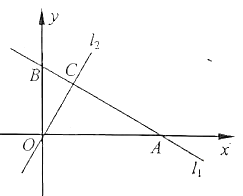
ЎҫМвДҝЎҝИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬Т»ҙОәҜКэ![]() өДНјПу
өДНјПу![]() ·ЦұрУл
·ЦұрУл![]() ЦбЎў
ЦбЎў![]() ЦбҪ»УЪ
ЦбҪ»УЪ![]() БҪөгЈ¬ХэұИАэәҜКэөДНјПу
БҪөгЈ¬ХэұИАэәҜКэөДНјПу![]() Ул
Ул![]() Ҫ»УЪөг
Ҫ»УЪөг![]() .
.
ЈЁ1Ј©Зуөг![]() ЧшұкЈ»
ЧшұкЈ»
ЈЁ2Ј©Зу![]() өДұнҙпКҪЈ»
өДұнҙпКҪЈ»
ЈЁ3Ј©Зу![]() әН
әН![]() өДГж»э.
өДГж»э.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ACКЗABCDөД¶ФҪЗПЯЈ¬ЎПBAC=ЎПDACЈ®

ЈЁ1Ј©ЗуЦӨЈәAB=BCЈ»
ЈЁ2Ј©ИфAB=2Ј¬AC=2![]() Ј¬ЗуABCDөДГж»эЈ®
Ј¬ЗуABCDөДГж»эЈ®
Ійҝҙҙр°ёәНҪвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com