
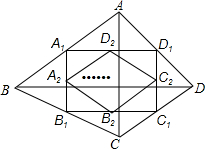
 如图,四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1,再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2,…,如此进行下去,得到四边形AnBnCnDn.下列结论正确的有( )
如图,四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1,再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2,…,如此进行下去,得到四边形AnBnCnDn.下列结论正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 首先根据题意,找出变化后的四边形的边长与四边形ABCD中各边长的长度关系规律,然后对以下选项作出分析与判断:
①根据矩形的判定与性质作出判断;
②根据菱形的判定与性质作出判断;
③由四边形的周长公式:周长=边长之和,来计算四边形A5B5C5D5的周长;
④根据四边形AnBnCnDn的面积与四边形ABCD的面积间的数量关系来求其面积.
解答 解:①连接A1C1,B1D1.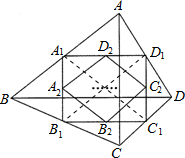 ∵在四边形ABCD中,顺次连接四边形ABCD 各边中点,得到四边形A1B1C1D1,
∵在四边形ABCD中,顺次连接四边形ABCD 各边中点,得到四边形A1B1C1D1,
∴A1D1∥BD,B1C1∥BD,C1D1∥AC,A1B1∥AC;
∴A1D1∥B1C1,A1B1∥C1D1,
∴四边形A1B1C1D1是平行四边形;
∵AC丄BD,∴四边形A1B1C1D1是矩形,
∴B1D1=A1C1(矩形的两条对角线相等);
∴A2D2=C2D2=C2B2=B2A2(中位线定理),
∴四边形A2B2C2D2是菱形;
故本选项错误;
②由①知,四边形A2B2C2D2是菱形;
∴根据中位线定理知,四边形A4B4C4D4是菱形;
故本选项正确;
③根据中位线的性质易知,A5B5=$\frac{1}{2}$A3B3=$\frac{1}{4}$A1B1=$\frac{1}{8}$AC,B5C5=$\frac{1}{2}$B3C3=$\frac{1}{4}$B1C1=$\frac{1}{8}$BD,
∴四边形A5B5C5D5的周长是2×$\frac{1}{8}$(a+b)=$\frac{a+b}{4}$,
故本选项正确;
④∵四边形ABCD中,AC=a,BD=b,且AC丄BD,
∴S四边形ABCD=ab÷2;
由三角形的中位线的性质可以推知,每得到一次四边形,它的面积变为原来的一半,
四边形AnBnCnDn的面积是$\frac{ab}{{2}^{n+1}}$,
故本选项正确.
综上所述,②③④正确.
故选C.
点评 本题主要考查了菱形的判定与性质、矩形的判定与性质及三角形的中位线定理(三角形的中位线平行于第三边且等于第三边的一半).解答此题时,需理清菱形、矩形与平行四边形的关系是最关键的.


科目:初中数学 来源: 题型:解答题
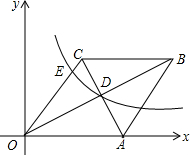 如图,在平面直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB,AC相交于D点,反比例函数y=$\frac{k}{x}$(x>0)经过D点,交BC的延长线于E点,且OB•AC=160,求反比例函数的解析式.
如图,在平面直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB,AC相交于D点,反比例函数y=$\frac{k}{x}$(x>0)经过D点,交BC的延长线于E点,且OB•AC=160,求反比例函数的解析式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
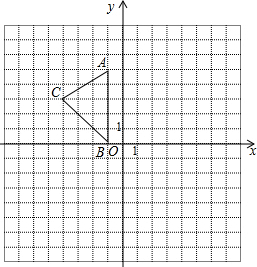 如图,在平面直角坐标系xOy中,A(-1,5),B(-1,0),C(-4,3).
如图,在平面直角坐标系xOy中,A(-1,5),B(-1,0),C(-4,3).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
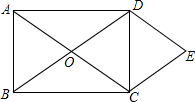 如图,长方形ABCD中,线段AC、BD相交于点O,DE∥AC,CE∥BD,BC=2cm,那么三角形EDC可以看作由△OAB平移得到的,连接OE,则OE=2cm.
如图,长方形ABCD中,线段AC、BD相交于点O,DE∥AC,CE∥BD,BC=2cm,那么三角形EDC可以看作由△OAB平移得到的,连接OE,则OE=2cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
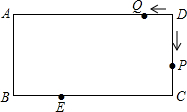 如图,在矩形ABCD中,AB=5cm,BC=10cm.动点P从点D出发,沿折线D-C-B-A-D以2cm/s的速度运动,动点Q从点D出发.沿D-A-B-C-D以1cm/s的速度运动.若动点P、Q同时出发,相遇是停止运动.设运动时间为ts.点E为BC边上一点,且BE=3cm.
如图,在矩形ABCD中,AB=5cm,BC=10cm.动点P从点D出发,沿折线D-C-B-A-D以2cm/s的速度运动,动点Q从点D出发.沿D-A-B-C-D以1cm/s的速度运动.若动点P、Q同时出发,相遇是停止运动.设运动时间为ts.点E为BC边上一点,且BE=3cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
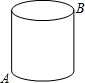 如图所示,有一个圆柱,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面的A点有一只蚂蚁,他想吃到上底面与A点相对的B点处的食物,沿圆柱侧面爬行的最短路程是多少?
如图所示,有一个圆柱,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面的A点有一只蚂蚁,他想吃到上底面与A点相对的B点处的食物,沿圆柱侧面爬行的最短路程是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com