
 如图,有一颗棋子放在图中的1号位置上,现按顺时针方向,第一次跳一步到2号位置上,第二次跳两步跳到4号位置上,第三次跳三步又跳到了1号位置上,第四次跳四步…一直进行下去,那么第2014次跳2014步就跳到了( )号位置上.
如图,有一颗棋子放在图中的1号位置上,现按顺时针方向,第一次跳一步到2号位置上,第二次跳两步跳到4号位置上,第三次跳三步又跳到了1号位置上,第四次跳四步…一直进行下去,那么第2014次跳2014步就跳到了( )号位置上.| A. | 1 | B. | 2 | C. | 4 | D. | 6 |
分析 棋子的跳法是有规律的,第一次跳1,第二次跳2,第三次跳3,…第n次跳n,则跳第n次后,棋子跳过的路程公式为:S=$\frac{1}{2}$n(n+1),棋子一个周期为6,设K=$\frac{S}{6}$,用K即可知道最后棋子的落位,若K为整数,则棋子落在1位;若K余1,则落2位,余2则落3位,余3则落4位,余4则落5位,余5则落6位.
解答 解:∵第一次跳一步,第二次跳两步,第三次跳三步,第四次跳四步…第2014次跳2014步,
∴2014次总共跳:1+2+3+4+…+2014=$\frac{1}{2}$×2014×(2014+1)=2029105,
2029105÷6=338184…1,
∵1步所对应的位置是2号位置,
∴第2014次跳2014步,所跳到的位置号是2号.
故选:B.
点评 此题考查图形的变化规律,找出数字之间的循环规律,利用规律解决问题.


科目:初中数学 来源: 题型:填空题
 如图,直线l:y=-2x-2与x轴、y轴分别交于A、B两点,向右平移直线l交第一象限内双曲线y=$\frac{k}{x}$于D、E,交x轴正半轴于C,CD交y轴于F点,若CD=AB,S△EOC=12,则k的值为6.
如图,直线l:y=-2x-2与x轴、y轴分别交于A、B两点,向右平移直线l交第一象限内双曲线y=$\frac{k}{x}$于D、E,交x轴正半轴于C,CD交y轴于F点,若CD=AB,S△EOC=12,则k的值为6.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
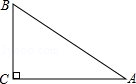 如图,已知斜坡AB的水平宽度是8米,斜坡AB的坡度为1:2,则斜坡AB的长为( )
如图,已知斜坡AB的水平宽度是8米,斜坡AB的坡度为1:2,则斜坡AB的长为( )| A. | 4$\sqrt{3}$ | B. | 4$\sqrt{5}$ | C. | 18 | D. | 8$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC,交AC于点E,交PC于点F,连接AF.
如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC,交AC于点E,交PC于点F,连接AF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
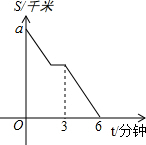 甲骑车到乙家研讨数学问题,中途因等候红灯停止了一分钟,之后又骑行了1.2千米到达了乙家.若甲骑行的速度始终不变,从出发开始计时,剩余的路程S(单位:千米)与时间t(单位:分钟)的函数关系的图象如图所示,则图中a等于( )
甲骑车到乙家研讨数学问题,中途因等候红灯停止了一分钟,之后又骑行了1.2千米到达了乙家.若甲骑行的速度始终不变,从出发开始计时,剩余的路程S(单位:千米)与时间t(单位:分钟)的函数关系的图象如图所示,则图中a等于( )| A. | 1.2 | B. | 2 | C. | 2.4 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AB=AC,DB⊥AB,DC⊥AC,且E,F,G,H分别为AB,AC,CD,BD的中点.
如图,在四边形ABCD中,AB=AC,DB⊥AB,DC⊥AC,且E,F,G,H分别为AB,AC,CD,BD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com