
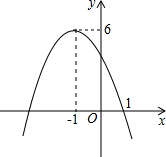 如图,已知抛物线y=ax2+bx+c,根据图象,回答下列问题:
如图,已知抛物线y=ax2+bx+c,根据图象,回答下列问题:分析 (1)根据顶点坐标和与x轴交点(1,0)可求出抛物线的解析式,从而得出a、b、c的值,并能计算出b2-4ac,a-b+c,4a2-2b+c的值;也可以利用图象确定a、b、c的符号,根据抛物线的个数确定b2-4ac的符号,根据x=-1时所对应的y值确定a-b+c的符号;
(2)先求出抛物线与x轴另一个交点的坐标,再根据图象写出不等式ax2+bx+c<0的解集,即y<0时,所对应的x的取值;
(3)抛物线与y=k有两个不同的交点,当k=6时,有一个交点,当k>6时,无交点,当k<6时,有两个交点,所以k<6.
解答 解:(1)由图象可知其顶点坐标为(-1,6),
∴可设抛物线解析式为y=a(x+1)2+6,
又∵图象过(1,0),
∴代入得:0=a(1+1)2+6,得a=-$\frac{3}{2}$,
∴y=-$\frac{3}{2}$(x+1)2+6=-$\frac{3}{2}$x2-3x+$\frac{9}{2}$,
∴a<0,b<0,c>0,
∵抛物线与x轴有两个交点,
∴△=b2-4ac>0,
由图可知:当x=-1时,y=6,即a-b+c=6>0,
4a2-2b+c=4×(-$\frac{3}{2}$)2-2×(-3)+$\frac{9}{2}$=9+6+$\frac{9}{2}$>0;
(2)由对称性得:抛物线与x轴另一个交点为(-3,0),
∴不等式ax2+bx+c<0的解集为x<-3或x>1;
(3)方程ax2+bx+c=k,有两个不相等的实根,相当于抛物线与y=k有两个不同的交点,
∴k<6.
点评 本题考查了二次函数与一元二次方程及不等式的关系,利用数形结合,解决问题;同时还考查了抛物线y=ax2+bx+c中,a,b,c,b2-4ac,a-b+c等符号的判别,可以通过计算解析式代入求得,也可以根据图象直接判别;这就需要熟练掌握以下几点:①二次项系数a决定抛物线的开口方向和大小.当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;
②一次项系数b和二次项系数a共同决定对称轴的位置. 当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.
③.常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c).
④抛物线与x轴交点个数.△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:解答题
 如图,给出一个任意的△ABC.
如图,给出一个任意的△ABC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在5×5的正方形网格中,每个小正方形的边长为1,请在所给网格中按下列要求画出图形.
如图,在5×5的正方形网格中,每个小正方形的边长为1,请在所给网格中按下列要求画出图形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
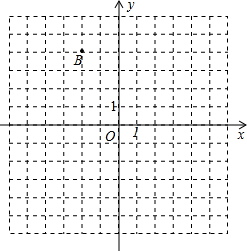 如图在直角坐标平面内,已知点A(-2,-3)与点B,将点A向右平移7个单位到达点C.
如图在直角坐标平面内,已知点A(-2,-3)与点B,将点A向右平移7个单位到达点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
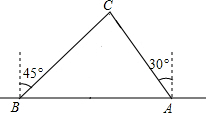 为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度,一天,我国两艘海监船刚好在某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域,如图,在B处测得C在东北方向上,在A处测得C在北偏西30°的方向上.
为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度,一天,我国两艘海监船刚好在某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域,如图,在B处测得C在东北方向上,在A处测得C在北偏西30°的方向上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
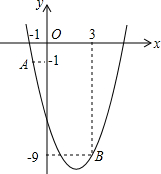 如图,已知抛物线y=ax2-4x+c的图象经过点A和点B.
如图,已知抛物线y=ax2-4x+c的图象经过点A和点B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com