
已知正方形 中,
中,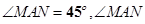 绕点
绕点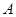 沿顺时针方向旋转,它的
沿顺时针方向旋转,它的
两边分别交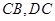 (或它们的延长线)于点
(或它们的延长线)于点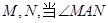 绕点
绕点 旋转到
旋转到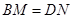 时(如图28①), 易证
时(如图28①), 易证
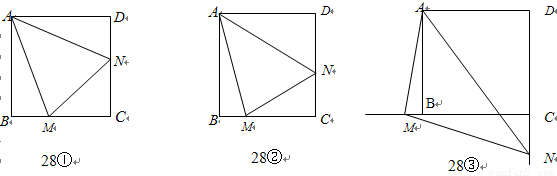
(1)当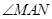 绕点
绕点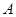 旋转到
旋转到 时(如图28②),线段
时(如图28②),线段 之间有怎样的数量关系?写出猜想,并加以证明;
之间有怎样的数量关系?写出猜想,并加以证明;
(2)当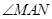 绕点
绕点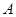 旋转到如图28③所示的位置时,线段
旋转到如图28③所示的位置时,线段 之间又有怎样的数量关系?请直接写出你的猜想.(9分)
之间又有怎样的数量关系?请直接写出你的猜想.(9分)
(1)BM+DN=MN,证明见解析(2)DN-BM=MN,证明见解析
【解析】(1)BM+DN=MN成立.
证明:如图,把△ADN绕点A顺时针旋转90°,
得到△ABE,则可证得E、B、M三点共线(图形画正确).
∴∠EAM=90°-∠NAM=90°-45°=45°,
又∵∠NAM=45°,
∴△AEM≌△ANM,
∴ME=MN,
∵ME=BE+BM=DN+BM,
∴DN+BM=MN;
(2)DN-BM=MN.
在线段DN上截取DQ=BM,
易证△AMN≌△AQN,
故MN=QN,
所以DN-BM=MN.


(1)BM+DN=MN成立,证得B、E、M三点共线即可得到△AEM≌△ANM,从而证得ME=MN.
(2)DN-BM=MN.证明方法与(1)类似.


科目:初中数学 来源: 题型:
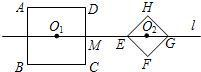 如图,已知正方形ABCD与正方形EFGH的边长分别是4
如图,已知正方形ABCD与正方形EFGH的边长分别是4| 2 |
| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:2012届黑龙江建三江分局九年级上学期期末调研数学试卷(带解析) 题型:解答题
已知正方形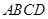 中,
中,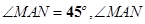 绕点
绕点 沿顺时针方向旋转,它的
沿顺时针方向旋转,它的
两边分别交 (或它们的延长线)于点
(或它们的延长线)于点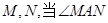 绕点
绕点 旋转到
旋转到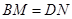 时(如图28①), 易证
时(如图28①), 易证

(1)当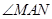 绕点
绕点 旋转到
旋转到 时(如图28②),线段
时(如图28②),线段 之间有怎样的数量关系?写出猜想,并加以证明;
之间有怎样的数量关系?写出猜想,并加以证明;
(2)当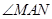 绕点
绕点 旋转到如图28③所示的位置时,线段
旋转到如图28③所示的位置时,线段 之间又有怎样的数量关系?请直接写出你的猜想.(9分)
之间又有怎样的数量关系?请直接写出你的猜想.(9分)
查看答案和解析>>
科目:初中数学 来源:第27章《二次函数》常考题集(24):27.3 实践与探索(解析版) 题型:解答题
 和
和 ,它们的中心O1,O2都在直线l上,AD∥l,EG在直线l上,l与DC相交于点M,ME=7-2
,它们的中心O1,O2都在直线l上,AD∥l,EG在直线l上,l与DC相交于点M,ME=7-2 ,当正方形EFGH沿直线l以每秒1个单位的速度向左平移时,正方形ABCD也绕O1以每秒45°顺时针方向开始旋转,在运动变化过程中,它们的形状和大小都不改变.
,当正方形EFGH沿直线l以每秒1个单位的速度向左平移时,正方形ABCD也绕O1以每秒45°顺时针方向开始旋转,在运动变化过程中,它们的形状和大小都不改变.
查看答案和解析>>
科目:初中数学 来源:2010年广东省广州市初中毕业生学业考试数学模拟试卷(二)(解析版) 题型:解答题
 和
和 ,它们的中心O1,O2都在直线l上,AD∥l,EG在直线l上,l与DC相交于点M,ME=7-2
,它们的中心O1,O2都在直线l上,AD∥l,EG在直线l上,l与DC相交于点M,ME=7-2 ,当正方形EFGH沿直线l以每秒1个单位的速度向左平移时,正方形ABCD也绕O1以每秒45°顺时针方向开始旋转,在运动变化过程中,它们的形状和大小都不改变.
,当正方形EFGH沿直线l以每秒1个单位的速度向左平移时,正方形ABCD也绕O1以每秒45°顺时针方向开始旋转,在运动变化过程中,它们的形状和大小都不改变.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com