
【题目】在平面直角坐标系中,如果某点的横坐标与纵坐标的和为10,则称此点为“合适点”例如,点(1,9),(﹣2019,2029)…都是“合适点”.
(1)求函数y=2x+1的图象上的“合适点”的坐标;
(2)求二次函数y=x2﹣5x﹣2的图象上的两个“合适点”A,B之间线段的长;
(3)若二次函数y=ax2+4x+c的图象上有且只有一个合适点”,其坐标为(4,6),求二次函数y=ax2+4x+c的表达式;
(4)我们将抛物线y=2(x﹣n)2﹣3在x轴下方的图象记为G1,在x轴及x轴上方图象记为G2,现将G1沿x轴向上翻折得到G3,图象G2和图象G3两部分组成的记为G,当图象G上恰有两个“合适点”时,直接写出n的取值范围.
【答案】(1)(3,7);(2)8![]() ;(3)y=﹣
;(3)y=﹣![]() x2+4x;(4)n<
x2+4x;(4)n<![]() 或10﹣
或10﹣![]() <n<10+
<n<10+![]()
【解析】
(1)根据“合适点”的定义,联立x+y=10和y=2x+1即可求解;
(2)根据“合适点”的定义,联立x+y=10和y=x2﹣5x﹣2即可求解;
(3)将点(4,6)代入二次函数表达式得:16a+16+c=6…①,联立y=10﹣x和y=ax2+4x+c并整理得:2x2+5x+(c﹣10)=0,△=25﹣4a(c﹣10)=0…②,联立①②即可求解;
(4)当直线m于图象G3只有一个交点时,直线m与图象G有3个“合适点”;当直线m经过点A、B时,直线m与图象G有3个“合适点”,即可求解.
解:(1)联立![]()
解得:![]()
故“合适点”的坐标为(3,7);
(2)联立![]()
解得:![]() 或
或![]()
故点A、B的坐标分别为:(﹣2,12)、(6,4),
则AB=![]() =8
=8![]() ;
;
(3)将点(4,6)代入二次函数表达式得:
16a+16+c=6…①,
联立y=10﹣x和y=ax2+4x+c并整理得:
ax2+5x+(c﹣10)=0,
由题意可知:△=25﹣4a(c﹣10)=0…②,
联立①②并解得:a=﹣![]() ,c=0,
,c=0,
故抛物线的表达式为:y=﹣![]() x2+4x;
x2+4x;
(4)图象G,如下图所示:
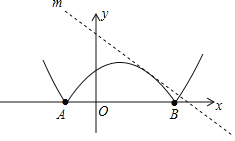
∵G1的顶点坐标为(n,-3),G1的函数表达式为:y=2(x﹣n)2-3,
∴G3的顶点坐标为(n,3),则G3的函数表达式为:y=﹣2(x﹣n)2+3,
x+y=10,则y=10﹣x,
设直线m为:y=10﹣x,
①当直线m与图象G3只有一个交点时,由图可知:直线m与G2有两个交点
直线m与图象G有3个交点,即有3个“合适点”,
联立直线m与G3的表达式得:y=﹣2(x﹣n)2+3=10﹣x,整理得:
2x2﹣(4n+1)x+(2n2+7)=0,
△=b2﹣4ac=8n﹣55=0,解得:n=![]() ,
,
故当n<![]() 时,图象G恰好有2个“合适点”;
时,图象G恰好有2个“合适点”;
②当直线m经过点A、B时,
直线m与图象G有3个交点,即有3个“合适点”,则在这两个点之间有2个“合适点”,
直线m与x轴的交点为(10,0),
将(10,0)代入y=2(x﹣n)2﹣3并解得:n=10![]() ,
,
故10﹣![]() <n<10+
<n<10+![]() ;
;
综上,n的取值范围为:n<![]() 或10﹣
或10﹣![]() <n<10+
<n<10+![]() .
.


科目:初中数学 来源: 题型:
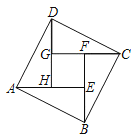
【题目】中国古代三国时期的数学家赵爽,创作了一幅“勾股弦方图”,通过数形结合,给出了勾股定理的详细证明如图,在“勾股弦方图”中,以弦为边长得到的正方形ABCD是由4个全等的直角三角形和中间的小正方形组成,这一图形被称作“赵爽弦图”张天同学要用细塑料棒制作“赵爽弦图”,若正方形ABCD与正方形EFCH的面积分别为169和49,则所用细塑料棒的长度为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(0,4),点B的坐标为(4,0),点C的坐标为(﹣4,0),点P在AB上,连结CP与y轴交于点D,连结BD.过P,D,B三点作⊙Q与y轴的另一个交点为E,延长DQ交⊙Q于点F,连结EF,BF.
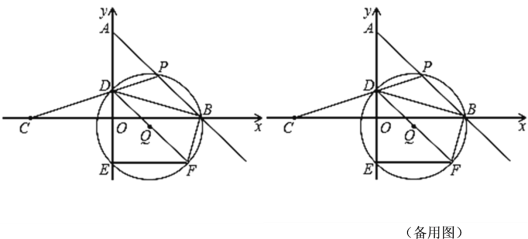
(1)求直线AB的函数解析式;
(2)求证:∠BDE=∠ADP;
(3)设DE=x,DF=y.请求出y关于x的函数解析式;
查看答案和解析>>
科目:初中数学 来源: 题型:
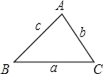
【题目】在△ABC中,∠A、∠B、∠C所对的边分别用a、b、c表示.
(1)如图,在△ABC中,∠A=2∠B,且∠A=60度.求证:a2=b(b+c).

(2)如果一个三角形的一个内角等于另一个内角的2倍,我们称这样的三角形为“倍角三角形”.第一问中的三角形是一个特殊的倍角三角形,那么对于任意的倍角三角形ABC,其中∠A=2∠B,关系式a2=b(b+c)是否仍然成立?并证明你的结论.
(3)试求出一个倍角三角形的三条边的长,使这三条边长恰为三个连续的正整数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:如果α,β都为锐角,且tanα=![]() ,tanβ=
,tanβ=![]() ,求α+β的度数.
,求α+β的度数.
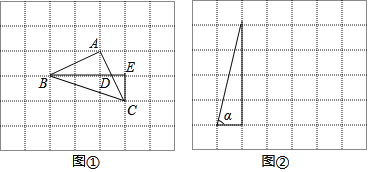
解决:如图①,把α,β放在正方形网格中,使得∠ABD=α,∠CBE=β,连结AC,易证△ABC是等腰直角三角形,因此可求得α+β=∠ABC= .
拓展:参考以上方法,解决下列问题:如果α,β都为锐角,当tanα=4,tanβ=![]() 时,
时,
(1)在图②的正方形网格中,利用已作出的锐角α,画出∠MON=α﹣β;
(2)求出α﹣β= °.
查看答案和解析>>
科目:初中数学 来源: 题型:
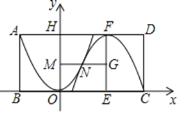
【题目】超市有一种“喜之郎“果冻礼盒,内装两个上下倒置的果冻,果冻高为4cm,底面是个直径为6cm的圆,轴截面可以近似地看作一个抛物线,为了节省成本,包装应尽可能的小,这个包装盒的长![]() 不计重合部分,两个果冻之间没有挤压
不计重合部分,两个果冻之间没有挤压![]() 至少为
至少为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,PA与⊙O相切于A点,点C是⊙O上的一点,且PC=PA.

(1)求证:PC是⊙O的切线;
(2)若∠BAC=45°,AB=4,求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①![]() ;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )

A. ①②③④ B. ①④ C. ②③④ D. ①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com