
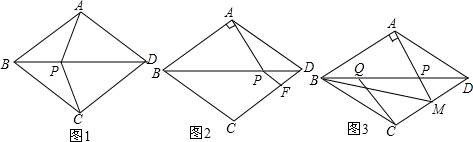
 ��ͼ����ABD�ǵ��������Σ�AB=AD������ABD��BD���۵á�CBD����P���߶�BD��һ�㣬
��ͼ����ABD�ǵ��������Σ�AB=AD������ABD��BD���۵á�CBD����P���߶�BD��һ�㣬���� ��1���ɷ��۵õ�������ֱ���жϳ���ADP�ա�CDP�����ɣ�
��2���ɣ�1������CP=AP���������ε���ǵ������������ڵ����ڽǵĺͼ�ƽ�ǵĶ����жϳ���CPF=��CFP���õ�CP=CF�����ɣ�
��3���ɣ�1���Ľ����жϳ��ı���ABCD�����Σ��̶��жϳ��ı���AQCPҲ�����Σ����ù��ɶ������MN���ɣ�
��� ֤������1���ɷ����У�AD=CD����ADP=��CDP��
�ڡ�ADP�͡�CDP�У�
$\left\{\begin{array}{l}{AD=CD}\\{��ADP=��CDP}\\{DP=DP}\end{array}\right.$
���ADP�ա�CDP��
��CP=AP��
��2������PC���ɣ�1���У�AP=CP��
�ɷ����С�BCP=��BAP=90�㣬
���CBP+��BPC=90�㣬
��AD=AB=CB=CD��
���CBP=��CDP��
���CDP+��BPC=90�㣬
�ߡ�DPF=45�㣬
���BPC+��CPF=135�㣬
���CPF=��CDP+45�㣬
�ߡ�CFP=��CDP+��BPF=��CDP+45�㣬
���CPF=��CFP��
��CP=CF��
��AD=CB=CF+FD=CP+FD=AP+FD��
��3����ͼ������AQ��AC��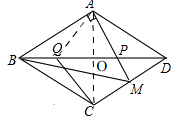
�ɣ�1���У�AQ=CQ��AP=CP���ɷ�����AB=BC��AD=CD��
��AB=AD��
��AB=BC=CD=AD��
���ı���ABCD�����Σ�
��AC��BD��OB=OD��OA=OC����BAD=120�㣬
��DQ=3BQ��
��BQ=OQ��
���ı���CPAQҲ�����Σ�
�ߡ�BAM=90�㣬��BAD=120�㣬
���BAQ=��DAM=30�㣬
���ABD=��CBD=��ADB=��CDB=30�㣬
�ߡ�ADM=60�㣬
���AMD=90�㣬
�ߡ�ACD�ȱ������Σ�
��CD=2DM��
��DM=x��
��CD=AD=AB=2DM=2x��AM=$\sqrt{3}$x��
��Rt��ABM��BM=$\frac{15}{2}$��
��AB2+AM2=BM2��
�ࣨ2x��2+��$\sqrt{3}$x��2=��$\frac{15}{2}$��2��
��x=$\frac{15\sqrt{7}}{14}$��x=-$\frac{15\sqrt{7}}{14}$���ᣩ��
��RT��AOB�У���ABD=30�㣬
��OA=$\frac{1}{2}$AB=x��OB=$\sqrt{3}$x��
��OQ=BQ=$\frac{1}{2}$OB=$\frac{\sqrt{3}}{2}$x��
��RT��AOQ��AQ=$\sqrt{O{A}^{2}+O{Q}^{2}}$=$\frac{\sqrt{7}}{2}$x=$\frac{15}{4}$��
��CQ=AQ=$\frac{15}{4}$��
���� �����Ǽ��α任�ۺ��⣬��Ҫ�����˷��۵����ʣ����ε��ж������ʣ������ε���ǵ��ص㣬�жϡ�CPF=��CFP�ǽⱾ��Ĺؼ���Ҳ���ѵ㣮


 һ����ʦ�����Ծ�ϵ�д�
һ����ʦ�����Ծ�ϵ�д� �����Ծ���Ԫ���Ծ�ϵ�д�
�����Ծ���Ԫ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4�� | B�� | 3�� | C�� | 2�� | D�� | 1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��3-��2=90�� | B�� | ��3+��2=90�� | C�� | ��3=��2 | D�� | û�й�ϵ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
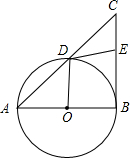 ��ͼ��Rt��ABC�У���ABC=90�㣬��ABΪֱ���ġ�O��AC�ڵ�D��EΪBC���е㣬����DE��OD��
��ͼ��Rt��ABC�У���ABC=90�㣬��ABΪֱ���ġ�O��AC�ڵ�D��EΪBC���е㣬����DE��OD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
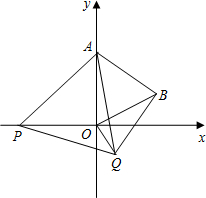 ��ƽ��ֱ������ϵ����ͼ����֪��A��0��2������P��x����һ���㣬���߶�APΪһ�ߣ������Ҳ����ȱ�������APQ������P�˶���ԭ��O��ʱ����Q��λ��ΪB����֪��ֱ������������ֱ�DZߵ�ƽ���͵���б�ߵ�ƽ������ֱ����������ֱ�DZ߳�Ϊa��b��б�߳�Ϊc����a2+b2=c2��
��ƽ��ֱ������ϵ����ͼ����֪��A��0��2������P��x����һ���㣬���߶�APΪһ�ߣ������Ҳ����ȱ�������APQ������P�˶���ԭ��O��ʱ����Q��λ��ΪB����֪��ֱ������������ֱ�DZߵ�ƽ���͵���б�ߵ�ƽ������ֱ����������ֱ�DZ߳�Ϊa��b��б�߳�Ϊc����a2+b2=c2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ֱ��y=x����A1����Ϊ��1��0��������A1��x��Ĵ��߽�ֱ��y=x�ڵ�B1����ԭ��OΪԲ�ģ�OB1��Ϊ�뾶������x���ڵ�A2���ٹ���A2��x��Ĵ��߽�ֱ��y=x�ڵ�B2����ԭ��OΪԲ�ģ�OB2��Ϊ�뾶������x���ڵ�A3���������մ�����������ȥ����B4��������Ϊ2$\sqrt{2}$��
��ͼ��ֱ��y=x����A1����Ϊ��1��0��������A1��x��Ĵ��߽�ֱ��y=x�ڵ�B1����ԭ��OΪԲ�ģ�OB1��Ϊ�뾶������x���ڵ�A2���ٹ���A2��x��Ĵ��߽�ֱ��y=x�ڵ�B2����ԭ��OΪԲ�ģ�OB2��Ϊ�뾶������x���ڵ�A3���������մ�����������ȥ����B4��������Ϊ2$\sqrt{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 1 | C�� | $\frac{1}{2}$ | D�� | 4 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com