
【题目】解答下列各题
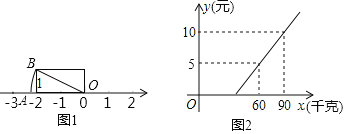
(1)如图1,已知OA=OB,数轴上的点A所表示的数为m,且|m+n|=2
①点A所表示的数m为 ;
②求代数式n2+m﹣9的值.
(2)旅客乘车按规定可以随身携带一定质量的行李,如果超过规定,则需购买行李票,设行李票y(元)是行李质量x(千克)的一次函数,其图象如图2所示.
①当旅客需要购买行李票时,求出y与x之间的函数关系式;
②如果张老师携带了42千克行李,她是否要购买行李票?如果购买需买多少行李票?
【答案】(1)①﹣![]() ;②3
;②3![]() 或﹣5
或﹣5![]() ;(2)①y=
;(2)①y=![]() x﹣5;②她要购买行李票,需买2元的行李票.
x﹣5;②她要购买行李票,需买2元的行李票.
【解析】
(1)①根据勾股定理可以求得OB的值,再根据OA=OB,即可得到m的值;
②根据m的值和|m+n|=2,可以得到n的值,从而可以得到n2+m﹣9的值;
(2)①根据函数图象利用待定系数法可以得到y与x的函数关系式;
②根据①中的函数关系式,将y=0,x=42分别代入计算,即可解答本题.
解:(1)①由图1可知,OA=OB,
∵OB=![]() =
=![]() ,
,
∴OA=![]() ,
,
∴点A表示的数m为﹣![]() ,
,
故答案为:﹣![]() ;
;
②∵|m+n|=2,m=﹣![]() ,
,
∴m+n=±2,m=﹣![]() ,
,
当m+n=2时,n=2+![]() ,则n2+m﹣9=(2+
,则n2+m﹣9=(2+![]() )2+(﹣
)2+(﹣![]() )﹣9=9+4
)﹣9=9+4![]() +(﹣
+(﹣![]() )﹣9=3
)﹣9=3![]() ;
;
当m+n=﹣2时,n=﹣2+![]() ,则n2+m﹣9=(﹣2+
,则n2+m﹣9=(﹣2+![]() )2+(﹣
)2+(﹣![]() )﹣9=9﹣4
)﹣9=9﹣4![]() +(﹣
+(﹣![]() )﹣9=﹣5
)﹣9=﹣5![]() ;
;
由上可得,n2+m﹣9的值是3![]() 或﹣5
或﹣5![]() ;
;
(2)①当旅客需要购买行李票时,设y与x之间的函数关系式为y=kx+b,
代入(60,5),(90,10)得:![]() ,解得:
,解得: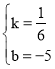 ,
,
∴当旅客需要购买行李票时,y与x之间的函数关系式是y=![]() x﹣5;
x﹣5;
②当y=0时,0=![]() x﹣5,得x=30,
x﹣5,得x=30,
当x=42时,y=![]() ×42﹣5=2,
×42﹣5=2,
故她要购买行李票,需买2元的行李票.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=![]() ,其中
,其中![]() 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小游在九寨沟开店做牛肉生意,根据协议,每天他会用![]() 元购进牦牛肉和费牛肉
元购进牦牛肉和费牛肉![]() 斤,其中牦牛肉和黄牛肉的数量之比为
斤,其中牦牛肉和黄牛肉的数量之比为![]() ,已知每斤牦牛肉的售价比每斤黄牛肉的售价多
,已知每斤牦牛肉的售价比每斤黄牛肉的售价多![]() 元,预计当天可全部售完.
元,预计当天可全部售完.
(1)若小游预计每天盈利不低于![]() 元,则牦牛肉每斤至少卖多少元?
元,则牦牛肉每斤至少卖多少元?
(2)若牦牛肉和黄牛肉均在(1)的条件下以最低价格销售,但8月份因为九寨沟地震,游客大量减少,导致牛肉滞销,小游决定降价销售每天进购的牛肉,已知牦牛肉的单价下降![]() (其中
(其中![]() ) ,但销量还是比进购数量下降了
) ,但销量还是比进购数量下降了![]() ,黄牛肉每斤下降了
,黄牛肉每斤下降了![]() 元,销量比进购数量下降了
元,销量比进购数量下降了![]() ,最终每天牦牛肉的销售额比黄牛肉销售额的
,最终每天牦牛肉的销售额比黄牛肉销售额的![]() 倍还多
倍还多![]() 元,求
元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线交于点O,点O又是正方形A1B1C1O的一个顶点,而且这两个正方形的边长相等.无论正方形A1B1C1O绕点O怎样转动,两个正方形重叠部分的面积,总等于一个正方形面积的( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
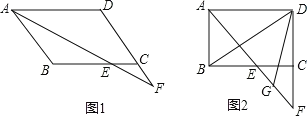
【题目】在ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
(1)在图1中说明CE=CF;
(2)若∠ABC=90°,G是EF的中点(如图2),求∠BDG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
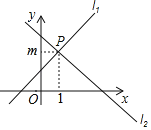
【题目】如图,直线l:y=x+2与直线l:y=kx+b相交于点P(1,m)
(1)写出k、b满足的关系;
(2)如果直线l:y=kx+b与两坐标轴围成一等腰直角三角形,试求直线l的函数表达式;
(3)在(2)的条件下,设直线l与x轴相交于点A,点Q是x轴上一动点,求当△APQ是等腰三角形时的Q点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,点E是BC边上一动点(点E不与点B、C重合),以线段DE为边长,作正方形DEFG,使得点F、G落在直线DE的下方,连接AF、BF.当△ABF为等腰三角形时,BE的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学家刘徽发展了“重差术”,用于测量不可到达的物体的高度,比如,通过下列步骤可测量山的高度PQ(如图):
(1)测量者在水平线上的A处竖立一根竹竿,沿射线QA方向走到M处,测得山顶P、竹竿顶端B及M在一条直线上;
(2)将该竹竿竖立在射线QA上的C处,沿原方向继续走到N处,测得山顶P、竹竿顶端D及N在一条直线上;
(3)设竹竿与AM、CN的长分别为![]() 、a1、a2,可得公式:PQ=
、a1、a2,可得公式:PQ=![]() +
+![]() .则上述公式中,d表示的是( )
.则上述公式中,d表示的是( )
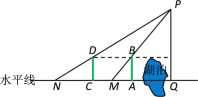
A. QA的长 B. AC的长 C. MN的长 D. QC的长
查看答案和解析>>
科目:初中数学 来源: 题型:
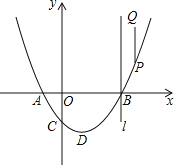
【题目】如图,已知抛物线![]() :
:![]() ,
,![]() 交x轴于A,
交x轴于A,![]() 点A在点B左边
点A在点B左边![]() ,交y轴于C,其顶点为D,P是
,交y轴于C,其顶点为D,P是![]() 上一个动点,过P沿y轴正方向作线段
上一个动点,过P沿y轴正方向作线段![]() 轴,使
轴,使![]() ,当P点在
,当P点在![]() 上运动时,Q随之运动形成的图形记为
上运动时,Q随之运动形成的图形记为![]() .
.
![]() 若
若![]() ,求点P运动到D点时点Q的坐标,并直接写出图形
,求点P运动到D点时点Q的坐标,并直接写出图形![]() 的函数解析式;
的函数解析式;
![]() 过B作直线
过B作直线![]() 轴,若直线l和y轴及
轴,若直线l和y轴及![]() ,
,![]() 所围成的图形面积为12,求t的值.
所围成的图形面积为12,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com