
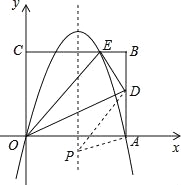
【题目】(2016广西省贺州市第26题)如图,矩形的边OA在x轴上,边OC在y轴上,点B的坐标为(10,8),沿直线OD折叠矩形,使点A正好落在BC上的E处,E点坐标为(6,8),抛物线y=ax2+bx+c经过O、A、E三点.
(1)求此抛物线的解析式;
(2)求AD的长;
(3)点P是抛物线对称轴上的一动点,当△PAD的周长最小时,求点P的坐标.
【答案】(1)、y=![]() ;(2)、AD=5;(3)、(5,
;(2)、AD=5;(3)、(5,![]() )
)
【解析】
试题分析:(1)、利用矩形的性质和B点的坐标可求出A点的坐标,再利用待定系数法可求得抛物线的解析式;(2)、设AD=x,利用折叠的性质可知DE=AD,在Rt△BDE中,利用勾股定理可得到关于x的方程,可求得AD的长;(3)、由于O、A两点关于对称轴对称,所以连接OD,与对称轴的交点即为满足条件的点P,利用待定系数法可求得直线OD的解析式,再由抛物线解析式可求得对称轴方程,从而可求得P点坐标.
试题解析:(1)∵四边形ABCD是矩形,B(10,8),
∴A(10,0), 又抛物线经过A、E、O三点,把点的坐标代入抛物线解析式可得
 ,解得
,解得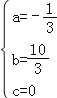 , ∴抛物线的解析式为y=﹣
, ∴抛物线的解析式为y=﹣![]() x2+
x2+![]() x;
x;
(2)、由题意可知:AD=DE,BE=10﹣6=4,AB=8, 设AD=x,则ED=x,BD=AB﹣AD=8﹣x,
在Rt△BDE中,由勾股定理可知ED2=EB2+BD2,即x2=42+(8﹣x)2,解得x=5, ∴AD=5;
(3)、∵y=﹣![]() x2+
x2+![]() x, ∴其对称轴为x=5, ∵A、O两点关于对称轴对称, ∴PA=PO,
x, ∴其对称轴为x=5, ∵A、O两点关于对称轴对称, ∴PA=PO,
当P、O、D三点在一条直线上时,PA+PD=PO+PD=OD,此时△PAD的周长最小,
如图,连接OD交对称轴于点P,则该点即为满足条件的点P,
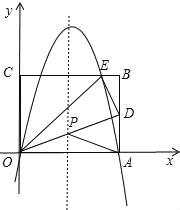
由(2)可知D点的坐标为(10,5),
设直线OD解析式为y=kx,把D点坐标代入可得5=10k,解得k=![]() , ∴直线OD解析式为y=
, ∴直线OD解析式为y=![]() x,
x,
令x=5,可得y=![]() , ∴P点坐标为(5,
, ∴P点坐标为(5,![]() ).
).


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合).现给出以下四个结论:(1)AE=CF;(2)△EPF是等腰直角三角形;(3)![]() ;(4)EF=AP.上述结论中始终正确的结论有( )
;(4)EF=AP.上述结论中始终正确的结论有( )
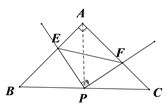
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
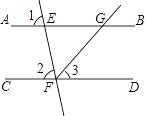
【题目】如图,已知直线AB、CD被直线EF所截,FG平分∠EFD,∠1=∠2=80°,求∠BGF的度数.
解:因为∠1=∠2=80°(已知),
所以AB∥CD__________
所以∠BGF+∠3=180°__________
因为∠2+∠EFD=180°(邻补角的性质).
所以∠EFD=________.(等式性质).
因为FG平分∠EFD(已知).
所以∠3=________∠EFD(角平分线的性质).
所以∠3=________.(等式性质).
所以∠BGF=________.(等式性质).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016浙江省舟山市第24题)小明的爸爸和妈妈分别驾车从家同时出发去上班,爸爸行驶到甲处时,看到前面路口时红灯,他立即刹车减速并在乙处停车等待,爸爸驾车从家到乙处的过程中,速度v(m/s)与时间t(s)的关系如图1中的实线所示,行驶路程s(m)与时间t(s)的关系如图2所示,在加速过程中,s与t满足表达式s=at2
(1)根据图中的信息,写出小明家到乙处的路程,并求a的值;
(2)求图2中A点的纵坐标h,并说明它的实际意义;
(3)爸爸在乙处等代理7秒后绿灯亮起继续前行,为了节约能源,减少刹车,妈妈驾车从家出发的行驶过程中,速度v(m/s)与时间t(s)的关系如图1中的折线O﹣B﹣C所示,行驶路程s(m)与时间t(s)的关系也满足s=at2,当她行驶到甲处时,前方的绿灯刚好亮起,求此时妈妈驾车的行驶速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M,N分别是AE,CD的中点。试探索BM和BN的关系,并证明你的结论。

查看答案和解析>>
科目:初中数学 来源: 题型:
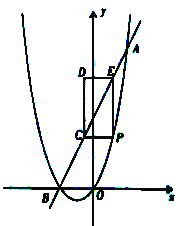
【题目】(2016贵州省毕节市第27题)如图,已知抛物线![]() 与直线
与直线![]() 交于A(a,8)、B两点,点P是抛物线上A、B之间的一个动点,过点P分别作
交于A(a,8)、B两点,点P是抛物线上A、B之间的一个动点,过点P分别作![]() 轴、
轴、![]() 轴的平行线与直线AB交于点C和点E.
轴的平行线与直线AB交于点C和点E.
(1)求抛物线的解析式;
(2)若C 为AB中点,求PC的长;
(3)如图,以PC,PE为边构造矩形PCDE,设点D的坐标为(m,n),请求出m,n之间的关系式。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com