
【题目】如图,在等腰梯形ABCD中,DC∥AB,E是DC延长线上的点,连接AE,交BC于点F.
(1)求证:△ABF∽△ECF;
(2)如果AD=5cm,AB=8cm,CF=2cm,求CE的长.
【答案】
(1)
证明:∵DC∥AB,
∴∠B=∠ECF,∠BAF=∠E,
∴△ABF∽△ECF.
(2)
解:∵在等腰梯形ABCD中,AD=BC,AD=5cm,AB=8cm,CF=2cm,
∴BF=3cm.
∵由(1)知,△ABF∽△ECF,
∴ ![]() ,即
,即 ![]() .
.
∴CE= ![]() (cm).
(cm).
【解析】(1)由“两直线平行,内错角相等”推知∠B=∠ECF,∠BAF=∠E.则由“两角法”证得结论;(2)利用(1)中的相似三角形的对应边成比例得到 ![]() ,即
,即 ![]() .所以CE=
.所以CE= ![]() (cm).
(cm).
【考点精析】认真审题,首先需要了解等腰梯形的性质(等腰梯形的两腰相等;同一底上的两个角相等;两条对角线相等),还要掌握相似三角形的判定与性质(相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方)的相关知识才是答题的关键.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】某游泳池有水4000m3 , 先放水清洗池子.同时,工作人员记录放水的时间x(单位:分钟)与池内水量y(单位:m3) 的对应变化的情况,如下表:
时间x(分钟) | … | 10 | 20 | 30 | 40 | … |
水量y(m3) | … | 3750 | 3500 | 3250 | 3000 | … |
(1)根据上表提供的信息,当放水到第80分钟时,池内有水多少m3?
(2)请你用函数解析式表示y与x的关系,并写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线a∥b,直线c与a、b都相交,从所标识的∠1、∠2、∠3、∠4、∠5这五个角中任意选取两个角,则所选取的两个角互为补角的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自古以来,钓鱼岛及其附属岛屿都是我国固有领土.如图,为了开发利用海洋资源,我勘测飞机测量钓鱼岛附属岛屿之一的北小岛(又称为鸟岛)两侧端点A、B的距离,飞机在距海平面垂直高度为100米的点C处测得端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了800米,在点D测得端点B的俯角为45°,求北小岛两侧端点A、B的距离.
(结果精确到0.1米,参考数 ![]() ≈1.73,
≈1.73, ![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l:y= ![]() x+1交x轴于点A,交y轴于点B,点A1、A2、A3 , …在x轴上,点B1、B2、B3 , …在直线l上.若△OB1A1 , △A1B2A2 , △A2B3A3 , …均为等边三角形,则△A5B6A6的周长是( )
x+1交x轴于点A,交y轴于点B,点A1、A2、A3 , …在x轴上,点B1、B2、B3 , …在直线l上.若△OB1A1 , △A1B2A2 , △A2B3A3 , …均为等边三角形,则△A5B6A6的周长是( )
A.24 ![]()
B.48 ![]()
C.96 ![]()
D.192 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,将抛物线C1:y=x2+3先向右平移1个单位,再向下平移7个单位得到抛物线C2 . C2的图象与x轴交于A、B两点(点A在点B的左侧).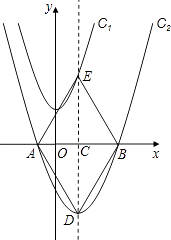
(1)求抛物线C2的解析式;
(2)若抛物线C2的对称轴与x轴交于点C,与抛物线C2交于点D,与抛物线C1交于点E,连结AD、DB、BE、EA,请证明四边形ADBE是菱形,并计算它的面积;
(3)若点F为对称轴DE上任意一点,在抛物线C2上是否存在这样的点G,使以O、B、F、G四点为顶点的四边形是平行四边形?如果存在,请求出点G的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图:∠1=∠2,∠3+∠4= 180°;确定直线a,c的位置关系,并说明理由;
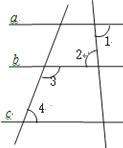
解:a c;
理由:∵∠1=∠2( ),
∴ a // ( );
∵ ∠3+∠4= 180°( ),
∴ c // ( );
∵ a // ,c // ,
∴ // ( );
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面四个整式中,不能表示图中阴影部分面积的是( )

A. (x+3)(x+2)﹣2x B. x(x+3)+6 C. 3(x+2)+x2 D. x2+5x
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com