
°æƒø°ø»ÁÕº£¨‘⁄![]() ÷–£¨
÷–£¨![]() £Æµ„
£Æµ„![]() ¥”µ„
¥”µ„![]() ≥ˆ∑¢£¨—ÿ
≥ˆ∑¢£¨—ÿ![]() ∑ΩœÚ“‘√ø√Î
∑ΩœÚ“‘√ø√Î![]() ∏ˆµ•Œª≥§∂»µƒÀŸ∂»œÚ÷’µ„
∏ˆµ•Œª≥§∂»µƒÀŸ∂»œÚ÷’µ„![]() ‘À∂Ø£®µ„
‘À∂Ø£®µ„![]() ≤ª”Î
≤ª”Î![]() ÷ÿ∫œ£©£¨π˝µ„
÷ÿ∫œ£©£¨π˝µ„![]() ◊˜
◊˜![]() Ωª’€œþ
Ωª’€œþ![]() ”⁄µ„
”⁄µ„![]() “‘
“‘![]() Œ™±þŒ œ¬◊˜’˝∑Ω–Œ
Œ™±þŒ œ¬◊˜’˝∑Ω–Œ![]() µ„
µ„![]() ¬‰‘⁄±þ
¬‰‘⁄±þ![]() …œ…˵„
…œ…˵„![]() ‘À∂صƒ ±º‰Œ™
‘À∂صƒ ±º‰Œ™![]() £®√Σ©£Æ
£®√Σ©£Æ

£®1£©÷±Ω””√∫¨![]() µƒ¥˙ ˝ Ω±Ì æœþ∂Œ
µƒ¥˙ ˝ Ω±Ì æœþ∂Œ![]() µƒ≥§£Æ
µƒ≥§£Æ
£®2£©µ±µ„![]() ¬‰‘⁄±þ
¬‰‘⁄±þ![]() …œ ±£¨«Û
…œ ±£¨«Û![]() µƒ÷µ£Æ
µƒ÷µ£Æ
£®3£©µ±’˝∑Ω–Œ![]() ”Î
”Î![]() ÷ÿµ˛≤ø∑÷Õº–ŒŒ™Àƒ±þ–Œ ±£¨…ËÀƒ±þ–Œµƒ√ʪ˝Œ™
÷ÿµ˛≤ø∑÷Õº–ŒŒ™Àƒ±þ–Œ ±£¨…ËÀƒ±þ–Œµƒ√ʪ˝Œ™![]() £®∆Ω∑Ωµ•Œª£©£¨«Û
£®∆Ω∑Ωµ•Œª£©£¨«Û![]() ”Î
”Î![]() ÷ƺ‰µƒ∫Ø ˝πÿœµ Ω£Æ
÷ƺ‰µƒ∫Ø ˝πÿœµ Ω£Æ
£®4£©µ„![]() Œ™±þ
Œ™±þ![]() µƒ÷–µ„£¨÷±Ω”–¥≥ˆ÷±œþ
µƒ÷–µ„£¨÷±Ω”–¥≥ˆ÷±œþ![]() Ω´’˝∑Ω–Œ
Ω´’˝∑Ω–Œ![]() ∑÷≥…µƒ¡Ω≤ø∑÷Õº–Œµƒ√ʪ˝±»Œ™
∑÷≥…µƒ¡Ω≤ø∑÷Õº–Œµƒ√ʪ˝±»Œ™![]() ±
±![]() µƒ÷µ£Æ
µƒ÷µ£Æ
°æ¥∞∏°ø£®1£©µ±![]() ±£¨
±£¨![]() £Æµ±
£Æµ±![]() ±£¨
±£¨![]() £ª£®2£©
£ª£®2£©![]() £ª£®3£©µ±
£ª£®3£©µ±![]() ±£Æ
±£Æ![]() £ªµ±
£ªµ±![]() ±£Æ
±£Æ![]() £ª£®4£©
£ª£®4£©![]() ªÚ
ªÚ![]()
°æΩ‚Œˆ°ø
£®1£©–Ë∑÷µ„Q‘⁄AB…œ∫ÕBC…œ¡Ω÷÷«Èøˆ£¨Ω·∫œ»ÒΩ«»˝Ω«∫Ø ˝º¥ø…«Ûµ√∂‘”¶µƒAPµƒ≥§£ª
£®2£©±Ì æ≥ˆAP£¨PN£¨NC£¨”√AB=AP+PN+NC£¨º¥ø…«Û≥ˆ£ª
£®3£©”…£®2£©÷™£¨–Ë∑÷Œ™![]() ªÚ
ªÚ![]() ¡Ω≤ø∑÷Ã÷¬€£ª
¡Ω≤ø∑÷Ã÷¬€£ª
£®4£©”…PF∑÷’˝∑Ω–Œ√ʪ˝Œ™1:2µƒ¡Ω≤ø∑÷£¨µ√≥ˆ±»¿˝πÿœµ£¨ π”√∆Ω––œþ∑÷œþ∂Œ≥…±»¿˝£¨º∆À„Ω·π˚£Æ
£®1£©◊˜![]() £¨¥π◊„Œ™D
£¨¥π◊„Œ™D
°þ![]() £¨BC=4£¨AB=3£¨
£¨BC=4£¨AB=3£¨
°ýAC=5
°þ![]()
°ý![]()
°ý![]()
°ý![]()
µ„Q‘⁄AB…œ ±£¨»ÁÕºÀ˘ æ
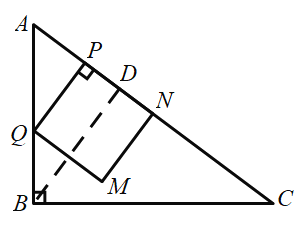
‘⁄![]() ÷–£¨BC=4£¨AB=3£¨
÷–£¨BC=4£¨AB=3£¨![]() £¨
£¨
‘⁄![]() ÷–£¨
÷–£¨![]() £¨‘Ú
£¨‘Ú![]() £®
£®![]() £©
£©
µ±µ„Q‘⁄BC…œ ±£¨»ÁÕºÀ˘ æ£∫
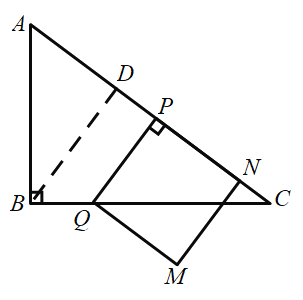
‘⁄![]() ÷–£¨BC=4£¨AB=3£¨
÷–£¨BC=4£¨AB=3£¨![]() £¨
£¨
‘⁄![]() ÷–£¨
÷–£¨![]() £¨‘Ú
£¨‘Ú![]() £®
£®![]() £©
£©
◊€…œ£∫µ±![]() ±£¨
±£¨![]() £Æµ±
£Æµ±![]() ±£¨
±£¨![]()
£®≤ª–¥»°÷µ∑∂Œß≤ªø€∑÷£©
£®2£©µ±µ„![]() ¬‰‘⁄±þ
¬‰‘⁄±þ![]() …œ ±£¨»ÁÕºÀ˘ æ
…œ ±£¨»ÁÕºÀ˘ æ
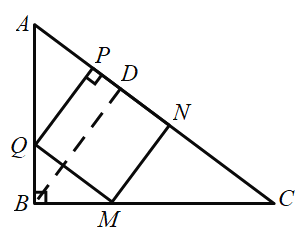
”…£®1£©÷™£¨![]() £¨
£¨![]()
‘⁄![]() ÷–£¨
÷–£¨![]()
°ýAB=AP+PN+NC=![]() Ω‚µ√
Ω‚µ√![]()
£®3£©”…£®2£©÷™£¨’˝∑Ω–Œ![]() ”Î
”Î![]() ÷ÿµ˛≤ø∑÷Õº–ŒŒ™Àƒ±þ–Œ ±
÷ÿµ˛≤ø∑÷Õº–ŒŒ™Àƒ±þ–Œ ±
![]() µƒ»°÷µ∑∂Œß «£∫
µƒ»°÷µ∑∂Œß «£∫![]() ªÚ
ªÚ![]()
µ±![]() ±£Æ¥À ±÷ÿ∫œ≤ø∑÷Œ™’˝∑Ω–ŒPQMN’˚㨑Ú
±£Æ¥À ±÷ÿ∫œ≤ø∑÷Œ™’˝∑Ω–ŒPQMN’˚㨑Ú![]()
µ±![]() ±£Æ»ÁÕºÀ˘ æ£∫
±£Æ»ÁÕºÀ˘ æ£∫
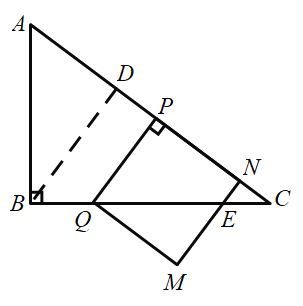
°ý![]() £¨
£¨![]()
‘⁄![]() ÷–£¨
÷–£¨![]()
°ý![]()
£®4£©µ±![]() ±£¨»ÁÕºÀ˘ æ£∫
±£¨»ÁÕºÀ˘ æ£∫

¥À ±![]()
÷±œþPFΩ´’˝∑Ω–ŒPQMN∑÷≥…1:2µƒ¡Ω≤ø∑÷£¨º¥![]()
°ý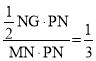 º¥
º¥![]() £¨
£¨
°ý![]()
‘⁄![]() ÷–£¨
÷–£¨![]() £¨
£¨
°ý![]()
◊˜![]() £¨¥π◊„Œ™H£¨
£¨¥π◊„Œ™H£¨
‘Ú![]()
”÷![]()
°ý![]()
°ý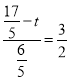 £¨Ω‚µ√
£¨Ω‚µ√![]()
µ±![]() ±£¨»ÁÕºÀ˘ æ£∫
±£¨»ÁÕºÀ˘ æ£∫

Õ¨…œø…÷™£∫![]()
”…![]() £¨µ√
£¨µ√![]()
”÷![]()
°ý![]() £¨º¥
£¨º¥![]()
”÷FŒ™BC÷–µ„
°ý![]() º¥
º¥![]()
°ý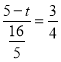 £¨Ω‚µ√
£¨Ω‚µ√![]()
◊€…œ£∫![]() ªÚ
ªÚ![]() £Æ
£Æ



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄∆Ω––Àƒ±þ–Œ![]() ÷–£¨µ„
÷–£¨µ„![]() ‘⁄
‘⁄![]() …œ£¨¡¨Ω”
…œ£¨¡¨Ω”![]() £¨
£¨![]() Œ™
Œ™![]() …œ“ªµ„£¨
…œ“ªµ„£¨![]() £Æ
£Æ
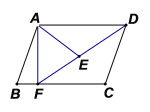
(1)«Û÷§£∫![]() °◊
°◊![]() £ª
£ª
(2)»Ù![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨«Û
£¨«Û![]() µƒ≥§£Æ
µƒ≥§£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄∆Ω––Àƒ±þ–ŒABCD÷–£¨µ„E‘⁄AD±þ…œ£¨¡¨Ω”BE°¢CE£¨EB∆Ω∑÷°œAEC .
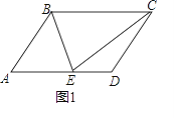
£®1£©»ÁÕº1£¨≈–∂œ°˜BCEµƒ–Œ◊¥£¨≤¢Àµ√˜¿Ì”…£ª
£®2£©»ÁÕº2£¨»Ù°œA=90°„£¨BC=5£¨AE=1£¨«Ûœþ∂ŒBEµƒ≥§£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ![]() ÷–£¨“—÷™µ„
÷–£¨“—÷™µ„![]() πÿ”⁄
πÿ”⁄![]() ÷·µƒ∂‘≥∆µ„
÷·µƒ∂‘≥∆µ„![]() £¨µ„
£¨µ„![]() «
«![]() ÷·…œµƒ“ª∏ˆ∂ص„£¨µ±
÷·…œµƒ“ª∏ˆ∂ص„£¨µ±![]() «µ»—¸»˝Ω«–Œ ±£¨
«µ»—¸»˝Ω«–Œ ±£¨![]() ÷µ∏ˆ ˝ «( )
÷µ∏ˆ ˝ «( )
A.1∏ˆB.2∏ˆC.3∏ˆD.4∏ˆ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄–¬π⁄◊¥≤°∂浃”∞œÏœ¬£¨ƒ≥—ß–£ª˝º´œÏ”¶’˛∏Æ∫≈’Ÿ£¨ø™’π¡À°∞Õ£øŒ≤ªÕ£—ß°±Õ¯…œ ⁄øŒπ§◊˜£¨Œ™¡ÀÕ¯…œ ⁄øŒπ§◊˜À≥¿˚ø™’π∫Õ»°µ√¡º∫√≥…–ߣ¨∏√–£‘⁄ ⁄øŒµ⁄“ª÷Ð∫Õ ⁄øŒµ⁄∂˛÷Ð∑÷±Àʪ˙≥È»°≤ø∑÷—ß…˙Ω¯––°∞Õ¯…œ ⁄øŒΩ×ߖßπ˚∑¥¿°°±Õ¯…œµ˜≤È£¨≤¢Ω´µ˜≤ÈΩ·π˚ªÊ÷∆≥…»Áœ¬¡Ω∑˘≤ªÕÍ’˚µƒÕ≥º∆Õº£¨µ˜≤Èœ‘ æ£∫¡Ω¥Œµ˜≤È∑¥¿°Ω×ߖßπ˚Œ™°∞Ωœ≤Ó°±»À ˝œýµ»£¨µ⁄∂˛÷Ð∑¥¿°Ω×ߖßπ˚Œ™°∞∫Ð∫√°±»À ˝±»¿˝±»µ⁄“ª÷Ð∂ý![]() £¨«Î∏˘æðµ˜≤Èœ‘ æ∫ÕÕ≥º∆Õº÷–µƒ–≈œ¢Ω‚戜¬¡–Œ £∫
£¨«Î∏˘æðµ˜≤Èœ‘ æ∫ÕÕ≥º∆Õº÷–µƒ–≈œ¢Ω‚戜¬¡–Œ £∫
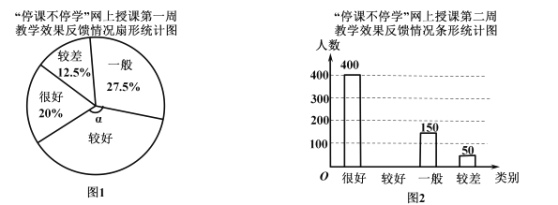
![]() ‘⁄Õº1÷–£¨±Ì æ°∞Ωœ∫√°±µƒ…»–Œ‘≤–ƒΩ«
‘⁄Õº1÷–£¨±Ì æ°∞Ωœ∫√°±µƒ…»–Œ‘≤–ƒΩ«![]() µƒ∂» ˝Œ™_ ∂»£¨≤¢∞—Õº2Ãı–ŒÕ≥º∆Õº≤π≥‰ÕÍ’˚£ª
µƒ∂» ˝Œ™_ ∂»£¨≤¢∞—Õº2Ãı–ŒÕ≥º∆Õº≤π≥‰ÕÍ’˚£ª
![]() »Ù∞—µ˜≤È∑¥¿°Ω×ߖßπ˚°∞∫Ð∫√°±∫Õ°∞Ωœ∫√°±◊˜Œ™Õ¯…œ ⁄øŒ≥…–ß¡º∫√µƒ±Í◊º£¨∏√–£¥Û‘º”–
»Ù∞—µ˜≤È∑¥¿°Ω×ߖßπ˚°∞∫Ð∫√°±∫Õ°∞Ωœ∫√°±◊˜Œ™Õ¯…œ ⁄øŒ≥…–ß¡º∫√µƒ±Í◊º£¨∏√–£¥Û‘º”–![]() √˚—ß…˙£¨«Îπ¿º∆ ⁄øŒµ⁄∂˛÷Зߖ£Õ¯…œ ⁄øŒ≥…–ß¡º∫√µƒ—ß…˙»À ˝£ª
√˚—ß…˙£¨«Îπ¿º∆ ⁄øŒµ⁄∂˛÷Зߖ£Õ¯…œ ⁄øŒ≥…–ß¡º∫√µƒ—ß…˙»À ˝£ª
![]() ”–“ªŒªº“≥§»œŒ™£¨¡Ω¥Œµ˜≤È∑¥¿° ⁄øŒ–ßπ˚Œ™°∞Ωœ≤Ó°±»À ˝œýµ»£¨“Ú¥À—ß–£‘⁄“ª÷Ð∫Ûµ˜’˚µƒ¥Î ©≤¢√ª”–÷∏þÕ¯…œ ⁄øŒ–ßπ˚£¨’‚Œªº“≥§∑÷Œˆ ˝æðµƒ∑Ω∑®∫œ¿Ì¬£ø«ÎΩ·∫œÕ≥º∆Õº£¨∂‘’‚Œªº“≥§∑÷Œˆ ˝æðµƒ∑Ω∑®º∞—ß–£‘⁄“ª÷Ð∫Ûµ˜’˚¥Î ©∂‘Õ¯…œ ⁄øŒ–ßπ˚µƒ”∞œÏÃ∏Ã∏ƒ„µƒø¥∑®£Æ
”–“ªŒªº“≥§»œŒ™£¨¡Ω¥Œµ˜≤È∑¥¿° ⁄øŒ–ßπ˚Œ™°∞Ωœ≤Ó°±»À ˝œýµ»£¨“Ú¥À—ß–£‘⁄“ª÷Ð∫Ûµ˜’˚µƒ¥Î ©≤¢√ª”–÷∏þÕ¯…œ ⁄øŒ–ßπ˚£¨’‚Œªº“≥§∑÷Œˆ ˝æðµƒ∑Ω∑®∫œ¿Ì¬£ø«ÎΩ·∫œÕ≥º∆Õº£¨∂‘’‚Œªº“≥§∑÷Œˆ ˝æðµƒ∑Ω∑®º∞—ß–£‘⁄“ª÷Ð∫Ûµ˜’˚¥Î ©∂‘Õ¯…œ ⁄øŒ–ßπ˚µƒ”∞œÏÃ∏Ã∏ƒ„µƒø¥∑®£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
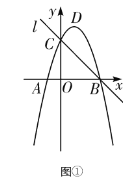
°æƒø°ø»ÁÕº£¨≈◊ŒÔœþy=ax2+bx+c£®a£¨b£¨c «≥£ ˝£¨a°Ÿ0£©”Îx÷·Ωª”⁄A£¨B¡Ωµ„£¨∂•µ„P£®m£¨n£©£Æ∏¯≥ˆœ¬¡–Ω·¬€£∫¢Ÿ2a+c£º0£ª¢⁄»Ù£®©Å![]() £¨y1£©£¨£®©Å
£¨y1£©£¨£®©Å![]() £¨y2£©£¨£®
£¨y2£©£¨£®![]() £¨y3£©‘⁄≈◊ŒÔœþ…œ£¨‘Úy1£æy2£æy3£ª¢€πÿ”⁄xµƒ∑Ω≥Ãax2+bx+k=0”– µ ˝Ω‚£¨‘Úk£æc©Ån£ª¢Ðµ±n=©Å
£¨y3£©‘⁄≈◊ŒÔœþ…œ£¨‘Úy1£æy2£æy3£ª¢€πÿ”⁄xµƒ∑Ω≥Ãax2+bx+k=0”– µ ˝Ω‚£¨‘Úk£æc©Ån£ª¢Ðµ±n=©Å![]() ±£¨°˜ABPŒ™µ»—¸÷±Ω«»˝Ω«–Œ£Æ∆‰÷–’˝»∑Ω·¬€ «______£®ÃÓ–¥–Ú∫≈£©£Æ
±£¨°˜ABPŒ™µ»—¸÷±Ω«»˝Ω«–Œ£Æ∆‰÷–’˝»∑Ω·¬€ «______£®ÃÓ–¥–Ú∫≈£©£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨Œ™º”øÏ5GÕ¯¬ÁΩ®…Ë£¨ƒ≥Õ®–≈π´Àæ‘⁄“ª∏ˆ∆¬∂»i£Ω1£∫2.4µƒ…Ω∆¬AB…œΩ®¡À“ª◊˘–≈∫≈À˛CD£¨–≈∫≈À˛µ◊∂ÀCµΩ…ΩΩ≈Aµƒæý¿ÎAC£Ω13√◊£¨‘⁄æý…ΩΩ≈AÀÆ∆Ωæý¿Î18√◊µƒE¥¶£¨”–“ª∏þ∂»Œ™10√◊µƒΩ®÷˛ŒÔEF£¨‘⁄Ω®÷˛ŒÔ∂•∂ÀF¥¶≤‚µ√–≈∫≈À˛∂•∂ÀDµƒ—ˆΩ«Œ™37°„£®–≈∫≈À˛º∞…Ω∆¬µƒ∆ √Ê∫ÕΩ®÷˛ŒÔµƒ∆ √Ê‘⁄Õ¨“ª∆Ω√Ê…œ£©£¨‘Ú–≈∫≈À˛CDµƒ∏þ∂»‘º «£®°°°°£©£®≤Œøº ˝æð£∫sin37°„°÷0.60£¨cos37°„°÷0.80£¨tan37°„°÷0.75£©
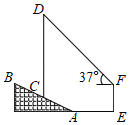
A.22.5√◊B.27.5√◊C.32.5√◊D.45.0√◊
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥—ß–£Œ™¡À¡ÀΩ‚æ≈ƒÍº∂—ß…˙…œ—ß∆⁄º‰∆Ωæ˘√øÃϵƒÀØ√þ«Èøˆ£¨œ÷¥”»´–£![]() √˚æ≈ƒÍº∂—ß…˙÷–Àʪ˙≥È»°¡À≤ø∑÷—ß…˙£¨µ˜≤È¡À’‚–©Õ¨—ß…œ—ß∆⁄º‰∆Ωæ˘√øÃϵƒÀØ√þ ±º‰
√˚æ≈ƒÍº∂—ß…˙÷–Àʪ˙≥È»°¡À≤ø∑÷—ß…˙£¨µ˜≤È¡À’‚–©Õ¨—ß…œ—ß∆⁄º‰∆Ωæ˘√øÃϵƒÀØ√þ ±º‰![]() £®µ•Œª£∫–° ±£©£¨≤¢∏˘æðµ˜≤ÈΩ·π˚¡–≥ˆÕ≥º∆±Ì£¨ªÊ÷∆≥……»–ŒÕ≥º∆Õº£¨»ÁÕºÀ˘ æ£Æ«Îƒ„∏˘æðÕº±ÌÃ·π©µƒ–≈œ¢Ω‚¥œ¬¡–Œ £∫
£®µ•Œª£∫–° ±£©£¨≤¢∏˘æðµ˜≤ÈΩ·π˚¡–≥ˆÕ≥º∆±Ì£¨ªÊ÷∆≥……»–ŒÕ≥º∆Õº£¨»ÁÕºÀ˘ æ£Æ«Îƒ„∏˘æðÕº±ÌÃ·π©µƒ–≈œ¢Ω‚¥œ¬¡–Œ £∫
∆Ωæ˘√øÃÏÀØ√þ ±º‰∑÷◊ÈÕ≥º∆±Ì
◊ȱ–Ú∫≈ | ÀØ√þ ±º‰ | »À ˝£®∆µ ˝£© |
|
|
|
|
|
|
|
|
|
|
|
|
∆Ωæ˘√øÃÏÀØ√þ ±º‰…»–ŒÕ≥º∆±Ì
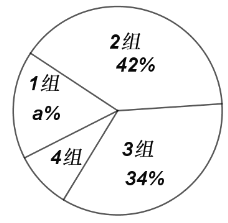
£®1£©![]() _______£¨
_______£¨![]() _______£¨
_______£¨![]() _______£®
_______£®![]() Œ™∞Ÿ∑÷∫≈«∞µƒ ˝◊÷£©£ª
Œ™∞Ÿ∑÷∫≈«∞µƒ ˝◊÷£©£ª
£®2£©Àʪ˙≥È»°µƒ’‚≤ø∑÷—ß…˙∆Ωæ˘√øÃÏÀØ√þ ±º‰µƒ÷–Œª ˝¬‰‘⁄_______◊È£®ÃÓ◊ȱ–Ú∫≈£©£ª
£®3£©π¿º∆»´–£![]() √˚æ≈ƒÍº∂—ß…˙÷–∆Ωæ˘√øÃÏÀØ√þ ±º‰≤ªµÕ”⁄
√˚æ≈ƒÍº∂—ß…˙÷–∆Ωæ˘√øÃÏÀØ√þ ±º‰≤ªµÕ”⁄![]() –° ±µƒ—ß…˙”–_______√˚£ª
–° ±µƒ—ß…˙”–_______√˚£ª
£®4£©»ÙÀ˘≥È≤ȵƒÀØ√þ ±º‰![]() £®–° ±£©µƒ
£®–° ±£©µƒ![]() √˚—ß…˙£¨∆‰÷–
√˚—ß…˙£¨∆‰÷–![]() √˚ƒ–…˙∫Õ
√˚ƒ–…˙∫Õ![]() √˚≈Æ…˙£¨œ÷¥”’‚
√˚≈Æ…˙£¨œ÷¥”’‚![]() √˚—ß…˙÷–Àʪ˙—°»°
√˚—ß…˙÷–Àʪ˙—°»°![]() √˚—ß…˙≤Œº”∏ˆ±∑√Ã∏£¨«Î”√¡–±ÌªÚª≠ ˜◊¥Õºµƒ∑Ω∑®«Û—°»°µƒ
√˚—ß…˙≤Œº”∏ˆ±∑√Ã∏£¨«Î”√¡–±ÌªÚª≠ ˜◊¥Õºµƒ∑Ω∑®«Û—°»°µƒ![]() √˚—ß…˙«°Œ™
√˚—ß…˙«°Œ™![]() ƒ–
ƒ–![]() ≈Ƶƒ∏≈¬ £Æ
≈Ƶƒ∏≈¬ £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº¢Ÿ£¨“—÷™≈◊ŒÔœþy£Ω![]() £´bx£´c”Îx÷·Ωª”⁄µ„A°¢
£´bx£´c”Îx÷·Ωª”⁄µ„A°¢![]() £¨”Îy÷·Ωª”⁄µ„
£¨”Îy÷·Ωª”⁄µ„![]() £¨÷±œþ
£¨÷±œþ![]() æ≠π˝B°¢C¡Ωµ„£Æ ≈◊ŒÔœþµƒ∂•µ„Œ™D£Æ
æ≠π˝B°¢C¡Ωµ„£Æ ≈◊ŒÔœþµƒ∂•µ„Œ™D£Æ
£®1£©«Û≈◊ŒÔœþ∫Õ÷±œþ![]() µƒΩ‚Œˆ Ω£ª
µƒΩ‚Œˆ Ω£ª
£®2£©≈–∂œ°˜BCDµƒ–Œ◊¥≤¢Àµ√˜¿Ì”…£Æ
£®3£©»ÁÕº¢⁄£¨»Ùµ„E «œþ∂ŒBC…œ∑Ωµƒ≈◊ŒÔœþ…œµƒ“ª∏ˆ∂ص„£¨π˝Eµ„◊˜EF°Õx÷·”⁄µ„F£¨EFΩªœþ∂ŒBC”⁄µ„G£¨µ±°˜ECG «÷±Ω«»˝Ω«–Œ ±£¨«Ûµ„Eµƒ◊¯±Í£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com