
����Ŀ������һ��ͼ�Σ�ͨ�����ֲ�ͬ�ķ�������������������Եõ�һ����ѧ��ʽ������ͼ1�����Եõ�![]() �����ʽ�������������⣺
�����ʽ�������������⣺
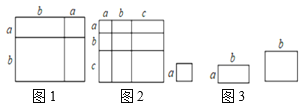
��1��д��ͼ2������ʾ����ѧ��ʽ ��
��2��������ʽ�˷������㷨��ͨ��������֤������ʽ��
��3�����ã�1���еõ��Ľ��ۣ������������⣺
��![]() ��
��![]() ����
����![]() ��
��
��4��С��ͬѧ��ͼ3��![]() �ű߳�Ϊ
�ű߳�Ϊ![]() �������Σ�
�������Σ�![]() �ű߳�Ϊ
�ű߳�Ϊ![]() �������Σ�
�������Σ�![]() �ų����ֱ�Ϊ
�ų����ֱ�Ϊ![]() ��
��![]() �ij�����ֽƬƴ��һ�����Ϊ
�ij�����ֽƬƴ��һ�����Ϊ![]() �ij����Σ���
�ij�������![]() ��
��
���𰸡�(1) ![]() (2)֤����������(3) 30; (4) 7.
(2)֤����������(3) 30; (4) 7.
��������
(1)������������=![]() ;��������=
;�����ε����=![]() ,�ɵõ�ʽ;
,�ɵõ�ʽ;
(2)���ö���ʽ�˶���ʽ���м��㼴��;
(3)����![]() ���м��㼴��;
���м��㼴��;
(4)������ƴͼ�ε����Ϊ:![]() , ��
, ��![]() ,���ɵõ�x, y, z��ֵ,�������.
,���ɵõ�x, y, z��ֵ,�������.
��: (1) ��������=![]() ;����������=
;����������=![]()
�ʴ�Ϊ:![]()
(2)֤��: (a+b+c) (a+b+c) ,
=![]() ,
,
=![]() .
.
(3)![]()
=![]() ,
,
=![]() ,
,
=30.
�ʴ�Ϊ: 30;
(4)�����֪����ƴͼ�ε����Ϊ:![]() ,
,
(2a+b) (a+4b)
=![]()
=![]()
��x=2��y=4, z=9.
��x+y+z=2+4+9=17.
�ʴ�Ϊ: 17.


 ������ϵ�д�
������ϵ�д� �±�Сѧ��Ԫ�Բ���ϵ�д�
�±�Сѧ��Ԫ�Բ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
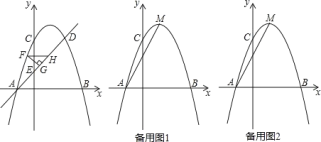
����Ŀ����ͼ�������� y����x2+bx+c �� x �ύ�� A��B ���㣬�� y �ύ�ڵ� C ���� A ������Ϊ(-1��0)���� C ������Ϊ(0��3)����D�͵� C ���������ߵĶԳ���Գƣ�ֱ�� AD �� y �ύ�ڵ� E ��
��1���������ߵĽ���ʽ��
��2����ͼ��ֱ�� AD �Ϸ�������������һ�� F������ F �� FG��AD �ڵ� G���� FH ƽ���� x �ύֱ�� AD �ڵ� H������FGH �ܳ������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
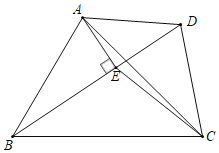
����Ŀ����ͼ�����ı���ABCD�У�tan��ABC��![]() ��BDΪ�Խ��ߣ���ABD+��BDC��90�㣬����A��AE��BD�ڵ�E������CE����AE��
��BDΪ�Խ��ߣ���ABD+��BDC��90�㣬����A��AE��BD�ڵ�E������CE����AE��![]() DE��EC��DC��5�����ABC�����Ϊ_____��
DE��EC��DC��5�����ABC�����Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
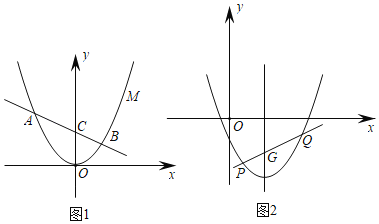
����Ŀ����ͼ1��������y��ax2������M��![]() ��
��![]() ������ֱ��AB��y��kx+1�ཻ��A��B���㣮
������ֱ��AB��y��kx+1�ཻ��A��B���㣮
��1����k����![]() �����ABO�������
�����ABO�������
��2����k����![]() �����������ϵĵ�P��ʹ�á�ABP������ǡ�ABO�������������P�����꣮
�����������ϵĵ�P��ʹ�á�ABP������ǡ�ABO�������������P�����꣮
��3��������������ƽ��������λ��������ƽ��������λ���õ�������C2������ͼ2��ֱ��y��kx��2��k+![]() ����������C2�ĶԳ��ύ��ΪG����������C2�Ľ���ΪP��Q���㣨��P�ڵ�Q����ࣩ����̽��
����������C2�ĶԳ��ύ��ΪG����������C2�Ľ���ΪP��Q���㣨��P�ڵ�Q����ࣩ����̽��![]() �Ƿ�Ϊ��ֵ����˵�����ɣ�
�Ƿ�Ϊ��ֵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
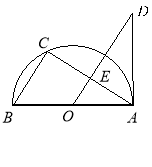
����Ŀ����ͼ��ABΪ��ԲO��ֱ������C�ڰ�ԲO�ϣ�����O��BC��ƽ���߽�AC�ڵ�E��������A��ֱ���ڵ�D������D=��BAC.
��1����֤��AD�ǰ�ԲO�����ߣ�
��2����BC=2��CE=![]() ����AD�ij�.
����AD�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵȱ���ABC�У�D��E��F�ֱ���BC��AC��AB�ϵĵ㣬DE��AC��EF��AB��
FD��BC������DEF���������ABC�����֮�ȵ����� ��

A��1��3 B��2��3 C��![]() ��2 D��
��2 D��![]() ��3
��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
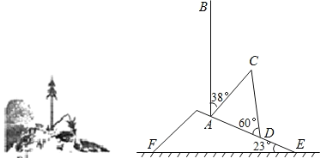
����Ŀ����ͼ��ʾ��ɽ������һ����ˮƽ�洹ֱ�Ĵ�����һ��̨�������������б���۶ϵ���ɽ���ϣ����Ķ���ǡ�ýӴ������森��֪ɽ�µ��½ǡ�AEF=23��������������б�ǡ�BAC=38�����������۶ϲ��ֺ��������ɵĽǡ�ADC=60����AD=4m������ô���û���۶�ǰ�ĸ߶ȣ�(�����ȷ����λ���ο����ݣ�![]() =1��4��
=1��4��![]() =1��7��
=1��7��![]() =2��4)��
=2��4)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
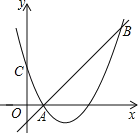
����Ŀ����ͼ�����κ���y=��x��2��2+m��ͼ����y�ύ�ڵ�C����B�ǵ�C���ڸö��κ���ͼ��ĶԳ���ԳƵĵ㣮��֪һ�κ���y=kx+b��ͼ���ö��κ���ͼ���ϵ�A��1��0������B��
��1������κ�����һ�κ����Ľ���ʽ��
��2������ͼ��д������kx+b����x��2��2+m��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
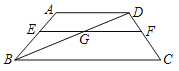
����Ŀ����ͼ��������ABCD�У���E��F�ֱ��ڱ�AB��CD�ϣ�AD��EF��BC��EF��BD���ڵ�G��AD��5��BC��10��![]() ��
��![]() ��
��
��1����EF�ij���
��2����![]() ��
��![]() ��
��![]() ��
��![]() ����ô
����ô![]() ���� ����
���� ����![]() ���� ������������
���� ������������![]() ��
��![]() ��ʾ��
��ʾ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com