
【题目】在正方形![]() 中,
中,![]() 是一条对角线,点
是一条对角线,点![]() 在直线
在直线![]() 上(不与点
上(不与点![]() 、
、![]() 重合),连接
重合),连接![]() ,平移
,平移![]() ,使点
,使点![]() 移动到点
移动到点![]() ,得到
,得到![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,
,![]() .
.
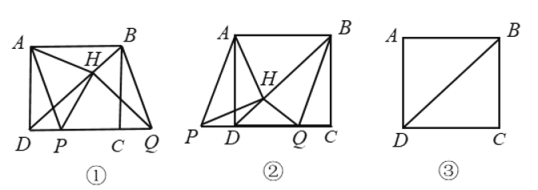
(问题发现)
(1)如图①,若点![]() 在线段
在线段![]() 上,
上,![]() 与
与![]() 的数量关系是________,位置关系是________.
的数量关系是________,位置关系是________.
(拓展探究)
(2)如图②,若点![]() 在线段
在线段![]() 的延长线上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给出证明,否则说明理由.
的延长线上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给出证明,否则说明理由.
(解决问题)
(3)若点![]() 在线段
在线段![]() 的延长线上,且
的延长线上,且![]() ,正方形
,正方形![]() 的边长为2,请直接写出求
的边长为2,请直接写出求![]() 的长度.
的长度.
【答案】(1)![]() ,
,![]() ;(2)结论仍然成立,理由见解析;(3)
;(2)结论仍然成立,理由见解析;(3)![]() .
.
【解析】
(1)连接HC,根据正方形的性质、等腰直角三角形的性质得到△HDP≌△HQC,根据全等三角形的性质得到HP=HC,∠DHP=∠QHC,根据正方形是轴对称图形证明结论;
(2)同(1)的证明方法相同,根据图形证明即可;
(3)由(1)的结论AH=PH,AH⊥PH,得出∠HPA=45°,推导出∠APD=30°,再由三角函数即可求解.
(1)![]() ,
,![]() .
.
证明如下:如解图,连接![]() ,
,
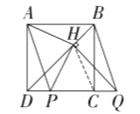
∵四边形![]() 是正方形,
是正方形,
∴∠![]() ,
,
又∵![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,![]() ,
,
由平移的性质可知![]() ,
,
在![]() 和
和![]() 中,
中,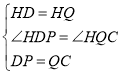 ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
根据正方形是轴对称图形得到![]() ,
,![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,![]() .
.
故答案为:![]() ,
,![]() ;
;
(2)(1)中的结论仍然成立,
理由如下:如解图,连接![]() ,
,

∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,
又∵![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,![]() ,
,
由平移的性质可知![]() ,
,
在![]() 和
和![]() 中,
中,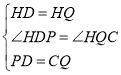 ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
根据正方形是轴对称图形得到![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ;
;
(3)![]() .
.
由(1)知,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() .
.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线L:y=ax2+bx+c与x轴交于A、B(3,0)两点(A在B的左侧),与y轴交于点C(0,3),已知对称轴x=1.
(1)求抛物线L的解析式;
(2)将抛物线L向下平移h个单位长度,使平移后所得抛物线的顶点落在△OBC内(包括△OBC的边界),求h的取值范围;
(3)设点P是抛物线L上任一点,点Q在直线l:x=﹣3上,△PBQ能否成为以点P为直角顶点的等腰直角三角形?若能,求出符合条件的点P的坐标;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形纸片ABCD,怎样折叠,能使边AB被三等分?
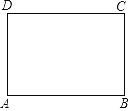
以下是小红的研究过程.
思考过程 | 要使边AB被三等分,若从边DC上考虑,就是要折出DM= 也就是要折出DM= 当DB、AM相交于F时,即要折出对角线上的DF= |
折叠方法和示意图 | ①折出DB;对折纸片,使D、B重合,得到的折痕与DB相交于点E;继续折叠纸片,使D、B与E重合,得到的折痕与DB分别相交于点F、G; ②折出AF、CG,分别交边CD、AB于M、Q; ③过M折纸片,使D落在MC上,得到折痕MN,则边AB被N、Q三等分.
|
(1)整理小红的研究过程,说明AN=NQ=QB;
(2)用一种与小红不同的方法折叠,使边AB被三等分.(需简述折叠方法并画出示意图)
查看答案和解析>>
科目:初中数学 来源: 题型:
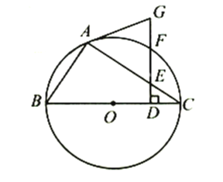
【题目】如图,![]() 为⊙
为⊙![]() 的内接三角形,
的内接三角形,![]() 为⊙
为⊙![]() 的直径,在线段
的直径,在线段![]() 上取点
上取点![]() (不与端点重合),作
(不与端点重合),作![]() ,分别交
,分别交![]() 、圆周于
、圆周于![]() 、
、![]() ,连接
,连接![]() ,已知
,已知![]() .
.
(1)求证:![]() 为⊙
为⊙![]() 的切线;
的切线;
(2)已知![]() ,填空:
,填空:
①当![]() __________
__________![]() 时,四边形
时,四边形![]() 是菱形;
是菱形;
②若![]() ,当
,当![]() __________时,
__________时,![]() 为等腰直角三角形.
为等腰直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的函数图象如图,点
的函数图象如图,点![]() 位于坐标原点,点
位于坐标原点,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在二次函数
在二次函数![]() 位于第一象限的图象上,
位于第一象限的图象上,![]() ,
,![]() ,
,![]() ,
,![]() …都是直角顶点在抛物线上的等腰直角三角形,则
…都是直角顶点在抛物线上的等腰直角三角形,则![]() 的斜边长为( )
的斜边长为( )

A.20B.![]() C.22D.
C.22D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年春季开学后,某校制定了《新冠肺炎疫情防控期间就餐规范》,条例规定:不对面就餐、食而不语、错峰就餐、鼓励打包等就餐措施.为了解学生对规范的认知程度,校园小记者随机调查部分同学,并根据调查结果绘制了如下两幅不完整的统计图表:

请根据以上图表,解答下列问题:
(1)这次被调查的同学共有______人,![]() ______,
______,![]() ______;
______;
(2)求扇形统计图中B部分所对圆心角度数;
(3)学校团委及政教处准备对“不太了解”及“毫不知情”的同学进行再学习培训,请问我校2400名学生中预计有多少人要接受再学习?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县教育局为了丰富初中学生的大课间活动,要求各学校开展形式多样的阳光体育活动.某中学就“学生体育活动兴趣爱好”的问题,随机调查了本校某班的学生,并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图:
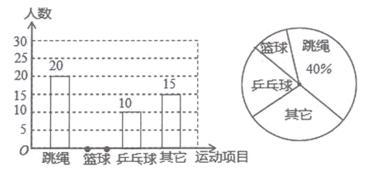
(1)在这次调查中,共调查了 人,在扇形统计图中,“乒乓球”的百分比为 %,如果学校有800名学生,估计全校学生中有 人喜欢篮球项目;
(2)请将条形统计图补充完整;
(3)学校在喜欢篮球的初一学生中挑选了3名同学,分别是李明、林海和陈阳,然后在这3名学生中最终挑选2人参加学校的篮球队,请用列表法或画树状图的方法求出李明最终被选上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形![]() 中,点
中,点![]() 为对角线
为对角线![]() 上一动点(点
上一动点(点![]() 与点
与点![]() 、
、![]() 不重合),连接
不重合),连接![]() ,作
,作![]() 交射线
交射线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() 、
、![]() ,作射线
,作射线![]() 交射线
交射线![]() 于点
于点![]()
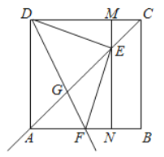
(1)求证:![]() ;
;
(2)当![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com