
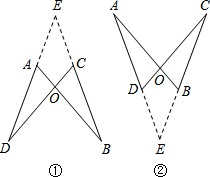
 问题:已知线段AB、CD相交于点O,AB=CD.连接AD、BC,请添加一个条件,使得△AOD≌△COB.
问题:已知线段AB、CD相交于点O,AB=CD.连接AD、BC,请添加一个条件,使得△AOD≌△COB.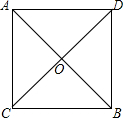 解:(1)可画出下面的反例:
解:(1)可画出下面的反例:

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2013届江苏省南京市白下区中考二模数学试卷(带解析) 题型:解答题
问题:已知线段AB、CD相交于点O,AB=CD.连接AD、BC,请添加一个条件,使得△AOD≌△COB.
小明的做法及思路
小明添加了条件:∠DAB=∠BCD.他的思路是:分两种情况画图①、图②,在两幅图中,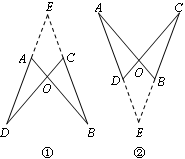
都作直线DA、BC,两直线交于点E.
由∠DAB=∠BCD,可得∠EAB=∠ECD.
∵AB=CD,∠E=∠E,
∴△EAB≌△ECD.∴EB=ED,EA=EC.
图①中ED-EA=EB-EC,即AD=CB.
图②中EA-ED=EC-EB,即AD=CB.
又∵∠DAB=∠BCD,∠AOD=∠COB,
∴△AOD≌△COB.
数学老师的观点:
(1)数学老师说:小明添加的条件是错误的,请你给出解释.
你的想法:
(2)请你重新添加一个满足问题要求的条件
,并说明理由.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省南京市白下区中考二模数学试卷(解析版) 题型:解答题
问题:已知线段AB、CD相交于点O,AB=CD.连接AD、BC,请添加一个条件,使得△AOD≌△COB.
小明的做法及思路
小明添加了条件:∠DAB=∠BCD.他的思路是:分两种情况画图①、图②,在两幅图中,
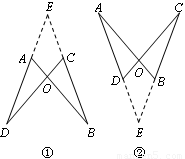
都作直线DA、BC,两直线交于点E.
由∠DAB=∠BCD,可得∠EAB=∠ECD.
∵AB=CD,∠E=∠E,
∴△EAB≌△ECD.∴EB=ED,EA=EC.
图①中ED-EA=EB-EC,即AD=CB.
图②中EA-ED=EC-EB,即AD=CB.
又∵∠DAB=∠BCD,∠AOD=∠COB,
∴△AOD≌△COB.
数学老师的观点:
(1)数学老师说:小明添加的条件是错误的,请你给出解释.
你的想法:
(2)请你重新添加一个满足问题要求的条件
,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
问题:已知线段AB、CD相交于点O,AB=CD.连接AD、BC,请添加一个条件,使得△AOD≌△COB.
 小明的做法及思路
小明的做法及思路
小明添加了条件:∠DAB=∠BCD.他的思路是:
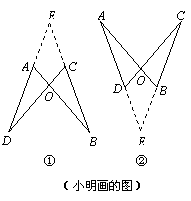 分两种情况画图①、图②,在两幅图中,
分两种情况画图①、图②,在两幅图中,
都作直线DA、BC,两直线交于点E.
由∠DAB=∠BCD,可得∠EAB=∠ECD.
∵AB=CD,∠E=∠E,
∴△EAB≌△ECD.∴EB=ED,EA=EC.
图①中ED-EA=EB-EC,即AD=CB.
图②中EA-ED=EC-EB,即AD=CB.
又∵∠DAB=∠BCD,∠AOD=∠COB,
∴△AOD≌△COB.
数学老师的观点
(1)数学老师说:小明添加的条件是错误的,请你给出解释.
你的想法
(2)请你重新添加一个满足问题要求的条件,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com