
【题目】6月5日是世界环境日,为了普及环保知识,增强环保意识,某市第一中学举行了“环保知识竞赛”,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频率分布表和不完整的频数分布直方图如下:

(1)直接写出a的值,并补全频数分布直方图.
分组 | 频数 | 频率 |
49.5~59.5 | 0.08 | |
59.5~69.5 | 0.12 | |
69.5~79.5 | 20 | |
79.5~89.5 | 32 | |
89.5~100.5 | a |
(2)若成绩在80分以上(含80分)为优秀,求这次参赛的学生中成绩为优秀的约为多少人?
(3)若这组被抽查的学生成绩的中位数是80分,请直接写出被抽查的学生中得分为80分的至少有多少人?
【答案】(1)0.28,
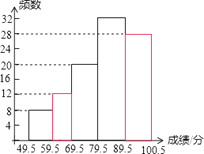 (2)600人(3)11人
(2)600人(3)11人
【解析】
(1)根据第一组的频数8与频率0.08,列式求出被抽取的学生的总人数,再根据频率求出第二组的频数,然后求出最后一组的频数,用频数除以被抽取的总人数即可得到a的值;根据计算补全统计图即可;
(2)用后两组的频率乘以参赛总人数1000,计算即可得解;
(3)根据中位数的定义,确定被抽取的100名学生中的第50与第51人都在第四组,可知第51人使这一组的第11人,从而得解.
解:(1)被抽取的学生总人数为:8÷0.08=100人,
59.569.5的频数为:100×0.12=12,
89.5100.5的频数为:1008122032=10072=28,
所以,a=![]() =0.28,
=0.28,
补全统计图如图;
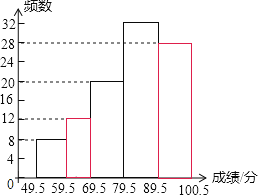
(2)成绩优秀的学生约为:![]() ×1000=600(人)
×1000=600(人)
答:成绩优秀的学生约为600人.
(3)根据统计表,第50人与第51人都在79.589.5一组,
∵中位数是80,而这一组的最低分是80,
∴得分为80分的至少有:5181220=5140=11(人).
答:被抽查的学生中得分为80分的至少有11人.


科目:初中数学 来源: 题型:
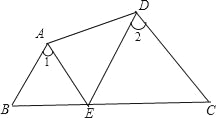
【题目】如图AB∥DE,∠1=∠2,试说明AE∥DC.下面是解答过程,请你填空或填写理由.
解:∵AB∥DE(已知)∴∠1= ( )
又∵∠1=∠2 (已知)∴∠2= (等量代换)
∴AE∥DC.( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上的点A表示的数为6,点B表示的数为﹣4,点C到点A、点B的距离相等,动点P从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为x(x大于0)秒.
(1)点C表示的数是 ;
(2)当x= 秒时,点P到达点A处?
(3)运动过程中点P表示的数是 (用含字母x的式子表示);
(4)当P,C之间的距离为2个单位长度时,求x的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC为直角梯形,A(4,0),B(3,4),C(0,4).点M从O出发以每秒2个单位长度的速度向A运动;点N从B同时出发,以每秒1个单位长度的速度向C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP垂直x轴于点P,连接AC交NP于Q,连接MQ.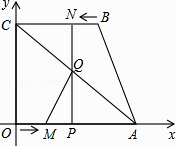
(1)点(填M或N)能到达终点;
(2)求△AQM的面积S与运动时间t的函数关系式,并写出自变量t的取值范围,当t为何值时,S的值最大;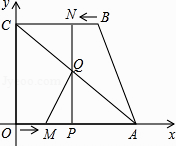
(3)是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣3x+3与x轴交于点B,与y轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线y= ![]() (k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线y=
(k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线y= ![]() (k≠0)上的点D1处,则a= .
(k≠0)上的点D1处,则a= . 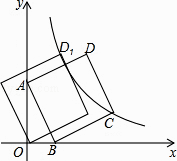
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1:y=kx+b平行于直线y=x﹣1,且与直线l2: ![]() 相交于点P(﹣1,0).
相交于点P(﹣1,0).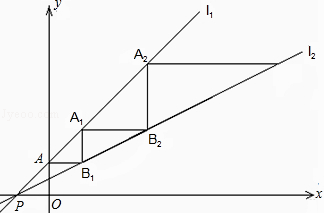
(1)求直线l1、l2的解析式;
(2)直线l1与y轴交于点A.一动点C从点A出发,先沿平行于x轴的方向运动,到达直线l2上的点B1处后,改为垂直于x轴的方向运动,到达直线l1上的点A1处后,再沿平行于x轴的方向运动,到达直线l2上的点B2处后,又改为垂直于x轴的方向运动,到达直线l1上的点A2处后,仍沿平行于x轴的方向运动,…
照此规律运动,动点C依次经过点B1 , A1 , B2 , A2 , B3 , A3 , …,Bn , An , …
①求点B1 , B2 , A1 , A2的坐标;
②请你通过归纳得出点An、Bn的坐标;并求当动点C到达An处时,运动的总路径的长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE相交于点H,已知EH=EB=6,AE=8,则CH的长是( )
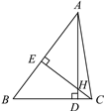
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系xOy中,把从点P出发沿纵或横方向到达点Q(至多拐一次弯)的路径长称为P,Q的“实际距离”.如图,若P(﹣1,1),Q(2,3),则P,Q的“实际距离”为5,即PS+SQ=5或PT+TQ=5.环保低碳的共享单车,正式成为市民出行喜欢的交通工具.设A,B,C三个小区的坐标分别为A(3,1),B(5,﹣3),C(﹣1,﹣5),若点M表示单车停放点,且满足M到A,B,C的“实际距离”相等,则点M的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴的正半轴相交,顶点在第四象限,对称轴为x=1,下列结论:①b<0;②a+b<0;③ ![]() <﹣2;④an2+bn=a(2﹣n)2+b(2﹣n)(n为任意实数),其中正确的结论个数是( )
<﹣2;④an2+bn=a(2﹣n)2+b(2﹣n)(n为任意实数),其中正确的结论个数是( ) 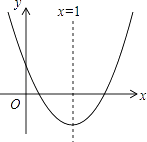
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com