
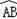 所在圆的圆心为O'时,求O'A的长度; ②如图2,当折叠后的
所在圆的圆心为O'时,求O'A的长度; ②如图2,当折叠后的 经过圆心为O时,求
经过圆心为O时,求 的长度; ③如图3,当弦AB=2时,求圆心O到弦AB的距离;
的长度; ③如图3,当弦AB=2时,求圆心O到弦AB的距离; 与
与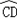 所在圆外切于点P时,设点O到弦AB.CD的距离之和为d,求d的值;②如图5,当AB与CD不平行,折叠后的
所在圆外切于点P时,设点O到弦AB.CD的距离之和为d,求d的值;②如图5,当AB与CD不平行,折叠后的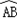 与
与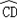 所在圆外切于点P时,设点M为AB的中点,点N为CD的中点,试探究四边形OMPN的形状,并证明你的结论.
所在圆外切于点P时,设点M为AB的中点,点N为CD的中点,试探究四边形OMPN的形状,并证明你的结论.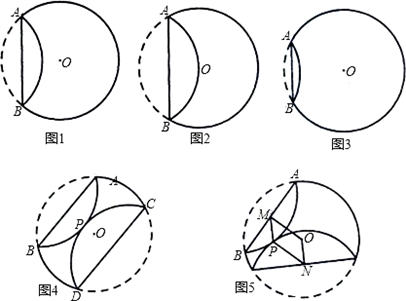
 所在圆O'与⊙O是等圆,∴O'A=OA=2;
所在圆O'与⊙O是等圆,∴O'A=OA=2; 经过圆O时,折叠后的
经过圆O时,折叠后的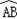 所在圆O'在⊙O上,
所在圆O'在⊙O上, =
=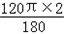 =
=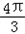 ;
;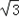 .
. 与
与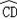 所在圆外切于点P时,过点O作EF⊥AB交AB于点H、交
所在圆外切于点P时,过点O作EF⊥AB交AB于点H、交 于点E,交CD于点G、交
于点E,交CD于点G、交 于点F,即点E、H、P、O、G、F在直径EF上,
于点F,即点E、H、P、O、G、F在直径EF上, D,
D, PE,PG=
PE,PG= PF,
PF, PE+
PE+ PF=
PF= (PE+PF)=2,
(PE+PF)=2,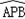 与
与 所在圆外切,
所在圆外切,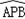 与
与 所在圆与⊙O是等圆,
所在圆与⊙O是等圆, OO''=ON,PM=ON,
OO''=ON,PM=ON,




科目:初中数学 来源: 题型:
 |
| AB |
 |
| AB |
 |
| AOB |
 |
| AB |
 |
| CD |
 |
| AB |
 |
| CD |
查看答案和解析>>
科目:初中数学 来源: 题型:
 |
| AB |
 |
| AB |
 |
| AB |
 |
| CD |
 |
| AB |
 |
| CD |
 |
| AB |
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(江西卷)数学(带解析) 题型:解答题
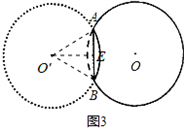
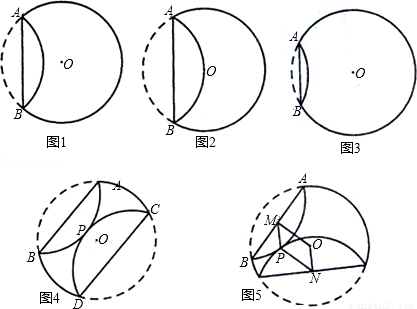
已知,纸片⊙O的半径为2,如图1,沿弦AB折叠操作.
(1)①折叠后的 所在圆的圆心为O′时,求O′A的长度;
所在圆的圆心为O′时,求O′A的长度;
②如图2,当折叠后的 经过圆心为O时,求
经过圆心为O时,求 的长度;
的长度;
③如图3,当弦AB=2时,求圆心O到弦AB的距离;
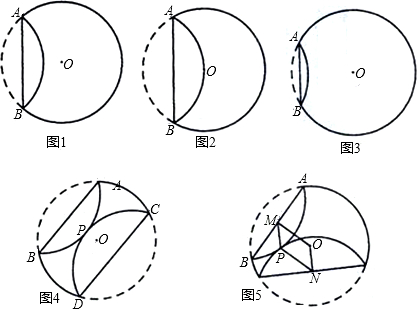
(2)在图1中,再将纸片⊙O沿弦CD折叠操作.
①如图4,当AB∥CD,折叠后的 与
与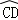 所在圆外切于点P时,设点O到弦AB.CD的距离之和为d,求d的值;
所在圆外切于点P时,设点O到弦AB.CD的距离之和为d,求d的值;
②如图5,当AB与CD不平行,折叠后的 与
与 所在圆外切于点P时,设点M为AB的中点,点N为CD的中点,试探究四边形OMPN的形状,并证明你的结论.
所在圆外切于点P时,设点M为AB的中点,点N为CD的中点,试探究四边形OMPN的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(江西卷)数学(解析版) 题型:解答题
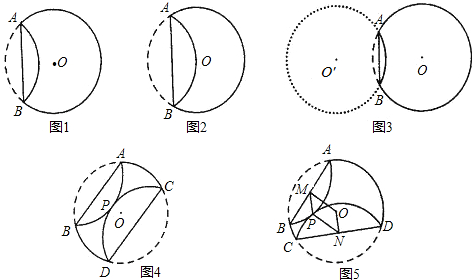
已知,纸片⊙O的半径为2,如图1,沿弦AB折叠操作.
(1)①折叠后的 所在圆的圆心为O′时,求O′A的长度;
所在圆的圆心为O′时,求O′A的长度;
②如图2,当折叠后的 经过圆心为O时,求
经过圆心为O时,求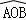 的长度;
的长度;
③如图3,当弦AB=2时,求圆心O到弦AB的距离;
(2)在图1中,再将纸片⊙O沿弦CD折叠操作.
①如图4,当AB∥CD,折叠后的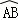 与
与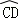 所在圆外切于点P时,设点O到弦AB.CD的距离之和为d,求d的值;
所在圆外切于点P时,设点O到弦AB.CD的距离之和为d,求d的值;
②如图5,当AB与CD不平行,折叠后的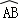 与
与 所在圆外切于点P时,设点M为AB的中点,点N为CD的中点,试探究四边形OMPN的形状,并证明你的结论.
所在圆外切于点P时,设点M为AB的中点,点N为CD的中点,试探究四边形OMPN的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源:2012年江西省南昌市中考数学试卷(解析版) 题型:解答题
 所在圆的圆心为O′时,求O′A的长度;
所在圆的圆心为O′时,求O′A的长度;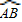 经过圆心为O时,求
经过圆心为O时,求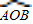 的长度;
的长度;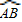 与
与 所在圆外切于点P时,设点O到弦AB、CD的距离之和为d,求d的值;
所在圆外切于点P时,设点O到弦AB、CD的距离之和为d,求d的值; 与
与 所在圆外切于点P时,设点M为AB的中点,点N为CD的中点,试探究四边形OMPN的形状,并证明你的结论.
所在圆外切于点P时,设点M为AB的中点,点N为CD的中点,试探究四边形OMPN的形状,并证明你的结论.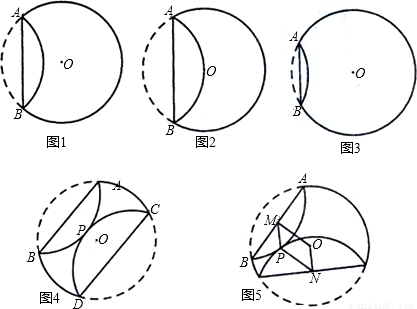
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com