
 如图,在?ABCD中,点E,F在对角线BD上,且四边形AFCE也是平行四边形,你能想办法推理出线段BE与DF相等吗?你有几种方法?并比较一下哪一种方法比较好.
如图,在?ABCD中,点E,F在对角线BD上,且四边形AFCE也是平行四边形,你能想办法推理出线段BE与DF相等吗?你有几种方法?并比较一下哪一种方法比较好. 分析 方法不唯一,可以通过证明三角形全等得到,也可以连接AC,交BD于点O.根据平行四边形的对角线互相平分的性质推知BO=DO,EO=FO;最后根据图形中线段间的和差关系即可证得结论.
解答 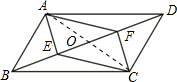 解:两种方法:1、通过证明△ABE≌CDF;2、利用平行四边形的性质:对角线互相平分即可证明BE=DF,
解:两种方法:1、通过证明△ABE≌CDF;2、利用平行四边形的性质:对角线互相平分即可证明BE=DF,
通过比较方法2较好,
理由如下:
连接AC,交BD于点O.
∵四边形ABCD和四边形AECF为平行四边形(已知),
∴BO=DO,EO=FO(平行四边形的对角线互相平分),
∴BO-EO=DO-FO,即BE=DF.
点评 本题考查了平行四边形的判定与性质.平行四边形的性质:①平行四边形的对边平行且相等;②平行四边形的对角相等;③平行四边形的对角线互相平分.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
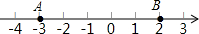 如图,数轴上的点A、B分别表示数-3、+2,若点C是AB的中点,则点C所表示的数是( )
如图,数轴上的点A、B分别表示数-3、+2,若点C是AB的中点,则点C所表示的数是( )| A. | 0 | B. | -$\frac{2}{3}$ | C. | -$\frac{1}{2}$ | D. | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com