
 小刚手里有一根长为80cm的木棒,他把木棒垂直放置在地面上(如图所示),此时测出该木棒在太阳光下的影子的长度为60cm,小刚绕木棒与地面的接触点转动该木棒,想尽办法使木棒的影子最长;问:该木棒转到什么位置时影子最长?并求出此时影子的长度.
小刚手里有一根长为80cm的木棒,他把木棒垂直放置在地面上(如图所示),此时测出该木棒在太阳光下的影子的长度为60cm,小刚绕木棒与地面的接触点转动该木棒,想尽办法使木棒的影子最长;问:该木棒转到什么位置时影子最长?并求出此时影子的长度. 分析 如图,OA=80cm,OB=60cm,AB为太阳光线,利用勾股定理可计算出AB=100,利用平行投影,当OA旋转到与太阳光线垂直时,此时木棒的影子最长,接着证明△AOB∽△OA′B′,然后利用相似比求出OB′即可.
解答 解:如图,OA=80cm,OB=60cm,AB为太阳光线,则AB=$\sqrt{6{0}^{2}+8{0}^{2}}$=100,
当OA旋转到与太阳光线垂直时,此时木棒的影子最长,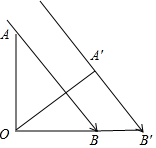
即OA′⊥A′B′(A′B′为太阳光线),
∵AB∥A′B′,
∴∠ABO=∠A′B′O,
∴△AOB∽△OA′B′,
∴OA:OA′=AB:OB′,
∴OB′=AB=100(cm),
答:该木棒转到与太阳光线垂直位置时影子最长,此时影子的长度为100cm.
点评 本题考查了相似三角形的应用:通常利用相似三角形的性质即相似三角形的对应边的比相等和“在同一时刻物高与影长的比相等”的原理解决.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案科目:初中数学 来源: 题型:解答题
 如图,点C是∠ABC一边上一点
如图,点C是∠ABC一边上一点查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 菱形和矩形 | B. | 菱形和正方形 | ||
| C. | 矩形和正方形 | D. | 平行四边形和菱形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 3 | D. | -3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com