
����Ŀ����ADE�У�AE=AD����EAD=90�㣮


��1����ͼ��1������EC��DB�ֱ�ƽ�֡�AED����ADE����AD��AE�ڵ�C��B������BC�������ж�AB��AC�Ƿ���ȣ���˵�����ɣ�
��2����ADE��λ�ñ��ֲ��䣬����1���еġ�ABC�Ƶ�A��ʱ����ת��ͼ
��2����λ�ã�CD��BE�ཻ��O�������ж��߶�BE��CD��λ�ù�ϵ��������ϵ����˵�����ɣ�
��3���ڣ�2���������£���CD=6�������ı���CEDB�������
���𰸡���1�����ɼ���������2�����ɼ���������3��18.
����������������1������֪�á�AEC=��ADB��AE=AD����A=��A�����á�ASA��֤����AEC�ա�ADB���ɣ���2��BE=CD��BE��CD������ת�����ʿ�֤��AEB�ա�ADC���Ӷ��ɵ�BE=CD�������ýǵ���ȹ�ϵ�������ϵ֤��BE��CD����3������BE��CD��BE=CD=6�����ı��εĶԽ����ഹֱʱ���ı��ε�������ڶԽ�����һ�룮
���������
(1)AB=AC.
�������£�
��EC��DB�ֱ�ƽ�֡�AED����ADE
���AEC=![]() ��AED,��ADB=
��AED,��ADB=![]() ��ADE
��ADE
�ߡ�AED=��ADE
���AEC=��ADB
�ڡ�AEC�͡�ADB�У�
��AEC=��ADB��AE=AD����A=��A
���AEC�ա�ADB
��AB=AC��
(2)BE=CD��BE��CD.
�������£�
�ߡ�EAD=��BAC
���EAB=��DAC
�ڡ�AEB�͡�ADC�У�
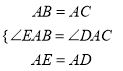 ��
��
���AEB�ա�ADC(SAS)
��EB=CD
���AEB=��ADC
�ߡ�AEB+��DEB+��ADE=90��
���ADC+��DEB+��ADE=90��
�ߡ�ADC+��DEB+��ADE+��DOE=180��
���DOE=90��
��BE��CD��
(3)�ı���CEDB�����=![]() ��BE��CD=
��BE��CD=![]()
![]() =18.
=18.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������У���ȷ���ǣ� ��.
A.ƽ��һ��ֱ�����ұش�ֱ������ֱ��.
B.ƽ��һ������ֱ�ߴ�ֱ�����������Ե���.
C.�ҵĴ��߱ؾ�������������Բ��Բ��.
D.��һ��Բ��ƽ��һ�����������Ե��ҵ�ֱ�߱ؾ������Բ��Բ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ����ֱ�Ķ�������l����һ��Ϊ1.5km����ͷMN�͵���C������C����ͷ�Ķ���N��20km�����ִ���36km/h���ٶȺ��У�����10��00��A����õ���Cλ���ִ��ı�ƫ��30�㷽������10��40��B����õ���Cλ���ִ��ı�ƫ��60�㷽���������C���12km��
��1�����ִ��մ��ٶ��뺽����ʱ���ﺣ���ߣ�
��2�����ִ����ı亽���ִ��ܷ�ͣ������ͷ����˵�����ɣ����ο����ݣ�![]() ��1.4��
��1.4��![]() ��1.7��
��1.7��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵������ȷ���ǣ�������
A. �������ĺͱش���ÿһ������ B. ���ȥһ�������������
C. ������κ�����Ϊ�� D. ��Ϊ�෴������������Ϊ0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��һ����λ����b��һ����λ��������������λ�����������λ����ǰ�棬���һ����λ�����������λ�����Ա�ʾΪ�� ��
A. ab B. 100a+b C. 1000a+b D. a+b
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ʾ������A����ƽ��5����λ���Ⱥ��غ���ͼ�е� ( )
A.��C
B.��F
C.��D
D.��E
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����˵�����⣺����a��b����ac��bc���Ǽ�����ķ����ǣ�������
A.c����1B.c��0C.c��2D.c��m2��mΪ����ʵ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A����2��y1����B����3��y2����������y����x��1��2+c�����㣬��y1_____y2������������������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ϱ�ʾ�����ĵ��Ϊ���㣬ij����ĵ�λ������1���ף�����������������⻭һ��15�����߶�AB����AB��ס��������ĸ������У� ����
A. 13��14�� B. 14��15�� C. 15��16�� D. 16��17��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com