练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．若|x+1|+（y+3）2=0，则（xy）2=9．

    分析 直接利用偶次方的性质结合绝对值的性质得出x，y的值进而得出答案．

    解答 解：∵|x+1|+（y+3）2=0，
    ∴x+1=0，y+3=0，
    解得：x=-1，y=-3，
    则（xy）2=[-1×（-3）]2=9．
    故答案为：9．

    点评 此题主要考查了偶次方的性质以及绝对值的性质，得出x，y的值是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    8．先阅读下列材料，然后回答问题：
    在一元二次方程ax2+bx+c=0（a≠0）中，若各项的系数之和为零，即a+b+c=0，则有一根为1，另一根为$\frac{c}{a}$．
    证明：设方程的两根为x1，x2，由a+b+c=0，
    知b=-（a+c），
    ∵x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{（a+c）±\sqrt{（a+c）^{2}-4ac}}{2a}$=$\frac{（a+c）±（a-c）}{2a}$
    ∴x1=1，x2=$\frac{c}{a}$．
    （1）若一元二次方程ax2+bx+c=0（a≠0）的各项系数满足a-b+c=0，则两根的情况怎样，试说明你的结论；
    （2）已知方程（ac-bc）x2+（bc-ab）x+（ab-ac）=0（abc≠0）有两个相等的实数根，运用上述结论证明：$\frac{2}{b}$=$\frac{1}{a}$+$\frac{1}{c}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．当0≤x≤2时，二次函数y=x2-2mx+m2+2m有最小值为3，则m的值为$\frac{3}{2}$或-3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．方程组$\left\{\begin{array}{l}{x-z=4}\\{z-2y=-1}\\{x+y-z=-1}\end{array}\right.$的解是（　　）
    A．$\left\{\begin{array}{l}{x=7}\\{y=-5}\\{z=-11}\end{array}\right.$B．$\left\{\begin{array}{l}{x=-7}\\{y=5}\\{z=-11}\end{array}\right.$C．$\left\{\begin{array}{l}{x=-7}\\{y=-5}\\{z=-11}\end{array}\right.$D．$\left\{\begin{array}{l}{x=7}\\{y=-5}\\{z=11}\end{array}\right.$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．2016年2月3日，广州恒大淘宝足球俱乐部官方宣布与西甲传统劲旅马德里竞技队神锋、哥伦比亚现役国脚马丁内斯正式签约，转会费为4200万欧元（约合人民币3.1亿元），签约四年，其中人民币3.1亿元用科学记数法可以表示为（　　）元．
    A．3.1×107B．3.1×108C．31×107D．0.31×109

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．若a2+|b-1|=0，则3a-4b=-4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

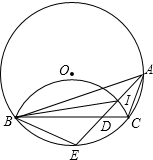    7．如图，已知△ABC内接于⊙O，点E在弧BC上，AE交BC于点D，EB2=ED•EA经过B、C两点的圆弧交AE于I．
    （1）求证：△ABE∽△BDE；
    （2）如果BI平分∠ABC，求证：$\frac{AB}{BD}$=$\frac{AE}{EI}$
    （3）设O的半径为5，BC=8，∠BDE=45°，求AD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

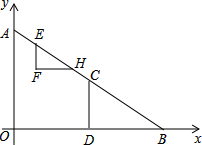    4．已知：在直角坐标系中，点A（0，6），B（8，0），点C是线段AB的中点，CD⊥OB交OB于点D，Rt△EFH的斜边EH在射线AB上，顶点F在射线AB的左侧，EF∥OA．点E从点A出发，以每秒1个单位的速度向点B运动，到点B停止．AE=EF，运动时间为t（秒）．
    （1）在Rt△EFH中，EF=t，EH=$\frac{5}{3}$t；F（$\frac{4}{5}$t，6-$\frac{8}{5}$t）（用含有t的代数式表示）
    （2）当点H与点C重合时，求t的值．
    （3）设△EFH与△CDB重叠部分图形的面积为S（S＞0），求S与t的关系式；
    （4）求在整个运动过程中Rt△EFH扫过的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

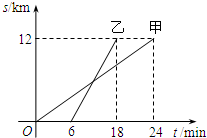    5．如图，表示甲、乙两人以相同路线前往离学校12千米的地方参加植树活动．甲、乙两人前往目的地所行驶的路程s（km）随时间t（min）变化的函数图象，则每分钟乙比甲多行驶的路程为（　　）
    A．1.5千米B．2千米C．0.5千米D．1千米

    查看答案和解析>>

    同步练习册答案