
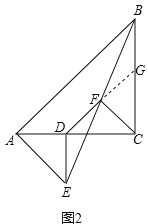
【题目】(10分)已知△ABC和△ADE是等腰直角三角形,∠ACB=∠ADE=90°,点F为BE中点,连结DF、CF.

(1)如图1, 当点D在AB上,点E在AC上,请直接写出此时线段DF、CF的数量关系和位置关系(不用证明);
(2)如图2,在(1)的条件下将△ADE绕点A顺时针旋转45°时,请你判断此时(1)中的结论是否仍然成立,并证明你的判断;
(3)如图3,在(1)的条件下将△ADE绕点A顺时针旋转90°时,若AD=1,AC=![]() ,求此时线段CF的长(直接写出结果).
,求此时线段CF的长(直接写出结果).
【答案】(1)相等和垂直;(2)成立,理由见试题解析;(3)![]() .
.
【解析】
试题分析:(1)根据“直角三角形斜边上的中线等于斜边的一半”可知DF=BF,根据∠DFE=2∠DCF,∠BFE=2∠BCF,得到∠EFD+∠EFB=2∠DCB=90°,DF⊥BF.
(2)延长DF交BC于点G,先证明△DEF≌△GCF,得到DE=CG,DF=FG,根据AD=DE,AB=BC,得到BD=BG又因为∠ABC=90°,所以DF=CF且DF⊥BF.
(3)延长DF交BA于点H,先证明△DEF≌△HBF,得到DE=BH,DF=FH,根据旋转条件可以△ADH为直角三角形,由△ABC和△ADE是等腰直角三角形,AC=![]() ,可以求出AB的值,进而可以根据勾股定理可以求出DH,再求出DF,由DF=BF,求出得CF的值.
,可以求出AB的值,进而可以根据勾股定理可以求出DH,再求出DF,由DF=BF,求出得CF的值.
试题解析:(1)∵∠ACB=∠ADE=90°,点F为BE中点,∴DF=![]() BE,CF=
BE,CF=![]() BE,∴DF=CF.
BE,∴DF=CF.
∵△ABC和△ADE是等腰直角三角形,∴∠ABC=45°,
∵BF=DF,∴∠DBF=∠BDF,
∵∠DFE=∠ABE+∠BDF,∴∠DFE=2∠DBF,
同理得:∠CFE=2∠CBF,
∴∠EFD+∠EFC=2∠DBF+2∠CBF=2∠ABC=90°,∴DF=CF,且DF⊥CF.
(2)(1)中的结论仍然成立.
证明:如图,此时点D落在AC上,延长DF交BC于点G.
∵∠ADE=∠ACB=90°,∴DE∥BC.∴∠DEF=∠GBF,∠EDF=∠BGF.
∵F为BE中点,∴EF=BF.∴△DEF≌△GBF.∴DE=GB,DF=GF.
∵AD=DE,∴AD=GB,
∵AC=BC,∴AC﹣AD=BC﹣GB,∴DC=GC.
∵∠ACB=90°,∴△DCG是等腰直角三角形,
∵DF=GF,∴DF=CF,DF⊥CF.
(3)延长DF交BA于点H,
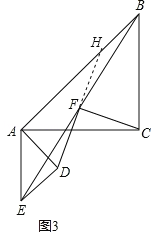
∵△ABC和△ADE是等腰直角三角形,∴AC=BC,AD=DE.∴∠AED=∠ABC=45°,
∵由旋转可以得出,∠CAE=∠BAD=90°,
∵AE∥BC,∴∠AEB=∠CBE,∴∠DEF=∠HBF.
∵F是BE的中点,∴EF=BF,∴△DEF≌△HBF,∴ED=HB,
∵AC=![]() ,在Rt△ABC中,由勾股定理,得:AB=4,
,在Rt△ABC中,由勾股定理,得:AB=4,
∵AD=1,∴ED=BH=1,∴AH=3,在Rt△HAD中由勾股定理,得:DH=![]() ,
,
∴DF=![]() ,∴CF=
,∴CF=![]() ,∴线段CF的长为
,∴线段CF的长为![]() .
.


科目:初中数学 来源: 题型:
【题目】直线MN与直线PQ垂直相交于O,点A在直线PQ上运动,点B在直线MN上运动. 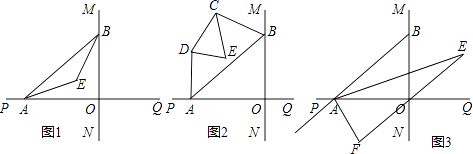
(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A,B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小.
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,点A,B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.
(3)如图3,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E,F,在△AEF中,如果有一个角是另一个角的3倍,试求∠ABO的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角平分线CF于点F.

(1)求证:AE=EF;
(2)如图2,若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”,其余条件不变,(1)中的结论是否仍然成立? ;(填“成立”或“不成立”);
(3)如图3,若把条件“点E是边BC的中点”改为“点E是边BC延长线上的一点”,其余条件仍不变,那么结论AE=EF是否成立呢?若成立请证明,若不成立说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知二次函数图象的顶点坐标为C(1,0),直线![]() 与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴
与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴![]() 上.
上.
(1)、求![]() 的值及这个二次函数的关系式;
的值及这个二次函数的关系式;
(2)、P为线段AB上的一个动点(点P与A、B不重合),过P作![]() 轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为
轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为![]() ,点P的横坐标为
,点P的横坐标为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)、D为直线AB与这个二次函数图象对称轴的交点,在线段AB上是否存在一点P,使得四边形DCEP是平行四边形?若存在,请求出此时P点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
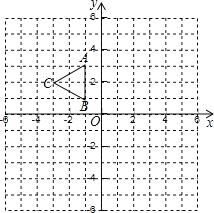
【题目】如图,△ABC三个定点坐标分别为A(﹣1,3),B(﹣1,1),C(﹣3,2).
(1)请画出△ABC关于y轴对称的△A1B1C1;
(2)以原点O为位似中心,将△A1B1C1放大为原来的2倍,得到△A2B2C2,请在第三象限内画出△A2B2C2,并求出S△A1B1C1:S△A2B2C2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了改善市区交通状况,计划修建一座新大桥,如图,新大桥的两端位于A、B两点,小张为了测量A、B之间的河宽,在垂直与新大桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82米.求AB的长(精确到0.1米,sin76.1°≈0.97,cos76.1°≈0.24,tan76.1°≈4.0;sin68.2°≈0.93,cos68.2°≈0.37,tan68.2°≈2.5.)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去年春季,蔬菜种植场在15公顷的大棚地里分别种植了茄子和西红柿,总费用是26.5万元.其中,种植茄子和西红柿每公顷的费用和每公顷获利情况如表:
每公顷费用(万元) | 每公顷获利(万元) | |
茄子 | 1.7 | 2.4 |
西红柿 | 1.8 | 2.6 |
请解答下列问题:
(1)求出茄子和西红柿的种植面积各为多少公顷?
(2)种植场在这一季共获利多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列去括号正确的是( )
A. a﹣(b﹣c)=a﹣b﹣c B. m﹣2(p﹣q)=m﹣2p+q
C. a+(b﹣c﹣2d)=a+b﹣c+2d D. x2﹣[﹣(﹣x+y)]=x2﹣x+y
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com