
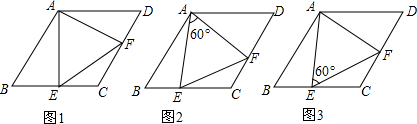
分析 (1)根据菱形的性质和等边三角形的判定方法得,△ABC是等边三角形.则AE⊥B,∠EAC=30°,同理∠CAF=30°,∠EAF=60°,再证明△ABE≌△ADF,得到AE=AF,则△AEF是等边三角形.
(2)连结AC,如图,根据菱形的性质得AB=BC,而∠B=60°,则可判定△ABC为等边三角形,得到∠2=60°,∠1+∠4=60°,AC=AB,易得∠ACF=60°,∠1=∠3,然后利用“ASA”可证明△AEB≌△AFC,于是得到AE=AF,即可解答;
(3)成立,作EG∥AB于G,则∠GEC=∠B=60°,先证明△ABC是等边三角形,∠BCF=120°,得出∠ACB=60°,再证明△GEC是等边三角形,得出EG=EC,∠EGC=60°,得出∠EAG=120°,证出∠1=∠2,由ASA证明△AEG≌△FEC,得出对应边相等即可,即可得到三角形AEF为等边三角形.
解答 解:(1)如图1,连接AC,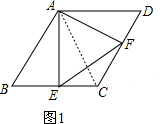
∵四边形ABCD是菱形,
∴AB=BC,∠B=∠D,
∵∠B=60°,
∴△ABC为等边三角形,
∴AC=AB=AD=CD,
∴∠CAD=60°,
∴∠BAD=120°,
∵E为BC的中点,
∴AE⊥BC,∠EAC=30°,
同理:∠CAF=30°
∴∠EAF=60°,
∵点E、F分别是边BC、CD边上的中点,BC=DC,
∴BE=DF,
在△ABE和△ADF中,
$\left\{\begin{array}{l}{AB=AD}\\{∠B=∠D}\\{BE=CF}\end{array}\right.$
∴△ABE≌△ADF,
∴AE=AF,
∵∠EAF=60°,
∴△AEF是等边三角形.
故答案为:等边.
(2)连结AC,如图2,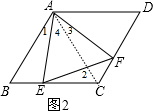
∵四边形ABCD为菱形,
∴AB=BC,
∵∠B=60°,
∴△ABC为等边三角形,
∴∠2=60°,∠1+∠4=60°,AC=AB,
∴∠ACF=60°,
∵∠EAF=60°,即∠3+∠4=60°,
∴∠1=∠3,
在△AEB和△AFC中,
$\left\{\begin{array}{l}{∠1=∠3}\\{AB=AC}\\{∠B=∠ACD}\end{array}\right.$,
∴△AEB≌△AFC,
∴AE=AF,
∵∠EAF=60°,
∴△AEF为等边三角形.
(3)成立,
连接AC,作EG∥AB交AC于点G,如图3所示:
则∠GEC=∠B=60°,
∵四边形ABCD是菱形,
∴AB=BC=CD=DA,∠D=∠B=60°,∠ACB=∠ACD,
∴△ABC是等边三角形,∠BCF=120°,
∴∠ACB=60°,
∴∠ACB=∠GEC=60°,
∴△GEC是等边三角形,
∴EG=EC,∠EGC=60°,
∴∠EAG=120°,
∵∠AEF=60°=∠GEC,
∴∠1=∠2,
在△AEG和△FEC中,
$\left\{\begin{array}{l}{∠1=∠2}\\{EG=EC}\\{∠EGA=∠ECF=12{0}^{°}}\end{array}\right.$,
∴△AEG≌△FEC(ASA),
∴AE=EF,
∵∠AEF=60°,
∴△AEF为等边三角形.
点评 本题考查了菱形的性质、等边三角形的判定与性质、全等三角形的判定与性质;熟练掌握菱形的性质,证明三角形全等和等边三角形是解决问题的关键.


 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源:2016-2017学年吉林省七年级下学期期中数学模拟试卷(四)(解析版) 题型:单选题
中国的光伏技术不断进步,电子元件的尺寸大幅度缩小,在芯片上某种电子元件大约只占0.000 000 7 mm2,这个数用科学记数法表示为( )
A. 7×10-6 mm2 B. 0.7×10-6 mm2 C. 7×10-7 mm2 D. 70×10-8 mm2
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
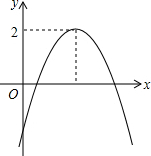 抛物线y=ax2+bx+c的图象如图,则关于x的方程ax2+bx-3=0的根的情况是( )
抛物线y=ax2+bx+c的图象如图,则关于x的方程ax2+bx-3=0的根的情况是( )| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=10,∠B=60°,BC=16,P、Q分别在边BC、AB上,且BP=BQ,连接PQ并延长与CA的延长线交于点R.
如图,在△ABC中,AB=10,∠B=60°,BC=16,P、Q分别在边BC、AB上,且BP=BQ,连接PQ并延长与CA的延长线交于点R.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
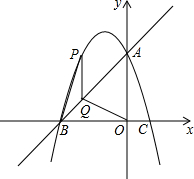 已知二次函数的图象与坐标轴交于A(0,3)、B(-3,0)、c(1,0).若点P是二次函数的图象上位于第二象限的点,过P作与y轴平行的直线与直线AB相交于点Q,则P点在何位置时,以线段BP、PO、OQ、QB围成的凹四边形的面积最大,并求最大值.
已知二次函数的图象与坐标轴交于A(0,3)、B(-3,0)、c(1,0).若点P是二次函数的图象上位于第二象限的点,过P作与y轴平行的直线与直线AB相交于点Q,则P点在何位置时,以线段BP、PO、OQ、QB围成的凹四边形的面积最大,并求最大值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
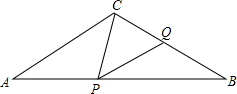 如图,在△ABC中,AC=BC=10,AB=16,点P在边AB上(不与点A,B重合),作∠CPQ=∠A,PQ交BC于Q,设AP=x,BQ=y.
如图,在△ABC中,AC=BC=10,AB=16,点P在边AB上(不与点A,B重合),作∠CPQ=∠A,PQ交BC于Q,设AP=x,BQ=y.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
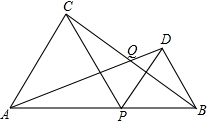 如图,已知线段AB的长为2a,点P是AB上的动点(点P不与A,B重合),分别以AP,PB为边向线段AB的同一侧作等边三角形APC和等边三角形PBD,连接AD,BC相交于点Q,设∠AQC=α,那么α的大小是否会随点P的移动而变化?请说明理由.
如图,已知线段AB的长为2a,点P是AB上的动点(点P不与A,B重合),分别以AP,PB为边向线段AB的同一侧作等边三角形APC和等边三角形PBD,连接AD,BC相交于点Q,设∠AQC=α,那么α的大小是否会随点P的移动而变化?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
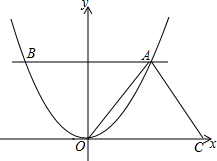 如图,A点是抛物线y=ax2上第一象限内的点,A点坐标为(3,6),AB⊥y轴与抛物线y=ax2的另一交点为B点.
如图,A点是抛物线y=ax2上第一象限内的点,A点坐标为(3,6),AB⊥y轴与抛物线y=ax2的另一交点为B点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com