
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:不详 题型:单选题

| A.m>0,n<2 | B.m>0,n>2 |
| C.m<0,n<2 | D.m<0,n>2 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 (亩)与补贴数额
(亩)与补贴数额 (元)之间成一次函数关系,且补贴与种植情况如下表:
(元)之间成一次函数关系,且补贴与种植情况如下表:| 补贴数额(元) | 10 | 20 | …… |
| 种植亩数(亩) | 160 | 240 | …… |
 的不断增大,种植规模也不断增加,但每亩牡丹的收益
的不断增大,种植规模也不断增加,但每亩牡丹的收益 (元)会相应降低,且该县补贴政策实施前每亩牡丹的收益为3000元,而每补贴10元(补贴数为10元的整数倍),每亩牡丹的收益会相应减少30元.
(元)会相应降低,且该县补贴政策实施前每亩牡丹的收益为3000元,而每补贴10元(补贴数为10元的整数倍),每亩牡丹的收益会相应减少30元. (亩)、每亩牡丹的收益
(亩)、每亩牡丹的收益 (元)与政府补贴数额
(元)与政府补贴数额 (元)之间的函数关系式;
(元)之间的函数关系式; (元)最大,又要从政府的角度出发,政府应将每亩补贴数额
(元)最大,又要从政府的角度出发,政府应将每亩补贴数额 定为多少元?并求出总收益
定为多少元?并求出总收益 的最大值和此时种植亩数;(总收益=每亩收益×亩数)
的最大值和此时种植亩数;(总收益=每亩收益×亩数) )
)查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 动.乙班先植树30棵,然后甲班才开始与乙班一起植树.设甲班植树的总量为
动.乙班先植树30棵,然后甲班才开始与乙班一起植树.设甲班植树的总量为 (棵),乙班植树的总量为
(棵),乙班植树的总量为 (棵),两班一起植树所用的时间(从甲班开始植树时计时)为
(棵),两班一起植树所用的时间(从甲班开始植树时计时)为 (时),
(时), 、
、 分别与
分别与 之间的部分函数图象如图9
之间的部分函数图象如图9 所示.
所示.
 、
、 与
与 之间的函数关系式;
之间的函数关系式; 时,甲、乙两班植树的总量之和能否超过
时,甲、乙两班植树的总量之和能否超过 棵.
棵.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的图象与x轴交于点A.与
的图象与x轴交于点A.与 轴交于点
轴交于点 ;二次函数
;二次函数 图象与一次函数y=
图象与一次函数y= 的图象交于
的图象交于 、
、 两点,与
两点,与 轴交于
轴交于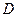 、
、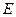 两点且
两点且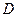 的坐标为
的坐标为

 轴上是否存在点P,使得△
轴上是否存在点P,使得△ 是直角三角形?若存在,求出所有的点
是直角三角形?若存在,求出所有的点 ,若不存在,请说明理由。
,若不存在,请说明理由。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com