
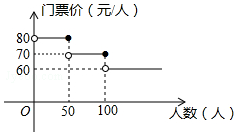
 我市某风景区门票价格如图所示,某旅行社有甲、乙两个旅行团队,计划在“五一”小黄金周期间到该景点游玩,两团队游客人数之和为120人,乙团队人数不超过50人.设甲团队人数为x人,如果甲、乙两团队分别购买门票,两团队门票款之和为W元.
我市某风景区门票价格如图所示,某旅行社有甲、乙两个旅行团队,计划在“五一”小黄金周期间到该景点游玩,两团队游客人数之和为120人,乙团队人数不超过50人.设甲团队人数为x人,如果甲、乙两团队分别购买门票,两团队门票款之和为W元.分析 (1)根据甲团队人数为x人,乙团队人数不超过50人,得到x≥70,分两种情况:①当70≤x≤100时,W=70x+80(120-x)=-10x+9600,②当100<x<120时,W=60x+80(120-x)=-20x+9600,即可解答;
(2)根据甲团队人数不超过100人,所以x≤100,由W=-10x+9600,根据70≤x≤100,利用一次函数的性质,当x=70时,W最大=8900(元),两团联合购票需120×60=7200(元),即可解答.
解答 解:(1)∵甲团队人数为x人,乙团队人数不超过50人,
∴120-x≤50,
∴x≥70,
①当70≤x≤100时,W=70x+80(120-x)=-10x+9600,
②当100<x<120时,W=60x+80(120-x)=-20x+9600,
综上所述,W=$\left\{\begin{array}{l}{-10x+9600(70≤x≤100)}\\{-20x+9600(100<x<120)}\end{array}\right.$;
(2)∵甲团队人数不超过100人,
∴x≤100,
∴W=-10x+9600,
∵70≤x≤100,
∴x=70时,W最大=8900(元),两团联合购票需120×60=7200(元),
∴最多可节约8900-7200=1700(元).
答:甲、乙两团队联合购票比分别购票最多可节约1700元.
点评 本题考查了一次函数的应用,解决本题的关键是根据题意,列出函数解析式,利用一次函数的性质求得最大值.注意确定x的取值范围.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
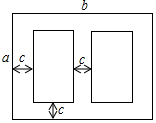 如图是某学校草场一角,在长为b米,宽为a米的长方形场地中间,有并排两个大小一样的篮球场,两个篮球场中间以及篮球场与长方形场地边沿的距离都为c米.
如图是某学校草场一角,在长为b米,宽为a米的长方形场地中间,有并排两个大小一样的篮球场,两个篮球场中间以及篮球场与长方形场地边沿的距离都为c米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
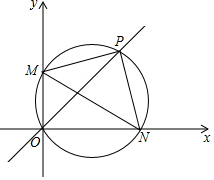 如图:M、N分别为直角坐标系x、y正半轴上两点,过M、N和原点O三点的圆和直线y=x交于点P,
如图:M、N分别为直角坐标系x、y正半轴上两点,过M、N和原点O三点的圆和直线y=x交于点P,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com