
【题目】在我国新型冠状病毒防控形势好转的态势下,各行各业复工复产所需的“消杀防护”设备成为急需物品.某医药超市库存的甲,乙两种型号“消杀防护”套装共![]() 套全部售完,售后统计甲型号套装每套的利润为
套全部售完,售后统计甲型号套装每套的利润为![]() 元,乙型号套装每套的利润为
元,乙型号套装每套的利润为![]() 元,两种型号“消杀防护"套装售完后的总利润为
元,两种型号“消杀防护"套装售完后的总利润为![]() 元
元
![]() 请计算本次销售中甲、乙两种型号“消杀防护”套装各销售了多少套.
请计算本次销售中甲、乙两种型号“消杀防护”套装各销售了多少套.
![]() 由于企业迫切需求,该医药超市决定再次购进
由于企业迫切需求,该医药超市决定再次购进![]() 套甲、乙两种型号的“消杀防护”套装,商场规定甲型号套装的采购数量不得超过乙型号的
套甲、乙两种型号的“消杀防护”套装,商场规定甲型号套装的采购数量不得超过乙型号的![]() 倍,请你通过计算说明如何采购才能让第二次销售获得最大利润.
倍,请你通过计算说明如何采购才能让第二次销售获得最大利润.
【答案】(1)本次销售中甲.乙两种型号的“消杀防护”套装均销售了![]() 套;(2)当购进甲型号“消杀防护”套装
套;(2)当购进甲型号“消杀防护”套装![]() 套,乙型号“消杀防护”套装
套,乙型号“消杀防护”套装![]() 套时,才能让第二次销售获得最大利润.
套时,才能让第二次销售获得最大利润.
【解析】
(1)设本次销售中甲型号“消杀防护”套装销售了![]() 套,乙型号“消杀防护”套装销售了
套,乙型号“消杀防护”套装销售了![]() 套,根据甲,乙两种型号“消杀防护”套装共
套,根据甲,乙两种型号“消杀防护”套装共![]() 套,甲型号套装每套的利润为
套,甲型号套装每套的利润为![]() 元,乙型号套装每套的利润为
元,乙型号套装每套的利润为![]() 元,两种型号“消杀防护"套装售完后的总利润为
元,两种型号“消杀防护"套装售完后的总利润为![]() 元,列出方程组,即可解答.
元,列出方程组,即可解答.
(2)设第二次购进甲型号“消杀防护”套装![]() 套,则购进乙型号“消杀防护”套装
套,则购进乙型号“消杀防护”套装![]() 套,第二次销售获得的利润为
套,第二次销售获得的利润为![]() 元,根据甲型号套装的采购数量不得超过乙型号的
元,根据甲型号套装的采购数量不得超过乙型号的![]() 倍,得出
倍,得出![]() ,再根据销售利润为
,再根据销售利润为![]() 即可求解.
即可求解.
![]() 设本次销售中甲型号“消杀防护”套装销售了
设本次销售中甲型号“消杀防护”套装销售了![]() 套,乙型号“消杀防护”套装销售了
套,乙型号“消杀防护”套装销售了![]() 套,依题意得:
套,依题意得:
![]()
解得![]()
答:本次销售中甲.乙两种型号的“消杀防护”套装均销售了![]() 套
套
![]() 设第二次购进甲型号“消杀防护”套装
设第二次购进甲型号“消杀防护”套装![]() 套,则购进乙型号“消杀防护”套装
套,则购进乙型号“消杀防护”套装![]() 套,第二次销售获得的利润为
套,第二次销售获得的利润为![]() 元,由题意可得:
元,由题意可得:
![]()
解得,![]() 且
且![]() 为大于
为大于![]() 的整数.
的整数.
销售利润为![]()
![]() .
.
![]() 随
随![]() 的增大而增大,
的增大而增大,
即当购进甲型号“消杀防护”套装![]() 套,乙型号“消杀防护”套装
套,乙型号“消杀防护”套装![]() 套时,才能让第二次销售获得最大利润.
套时,才能让第二次销售获得最大利润.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
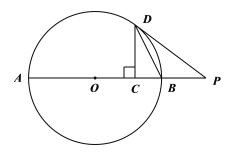
【题目】如图,点D在⊙O上,过点D的切线交直径AB的延长线于点P,DC⊥AB于点C.
(1)求证:DB平分∠PDC;
(2)如果DC = 6,![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某校落实新课改精神的情况,现以该校九年级二班的同学参加课外活动的情况为样本,对其参加“球类”、“绘画类”、“舞蹈类”、“音乐类”、“棋类”活动的情况进行调查统计,并绘制了如图所示的统计图.
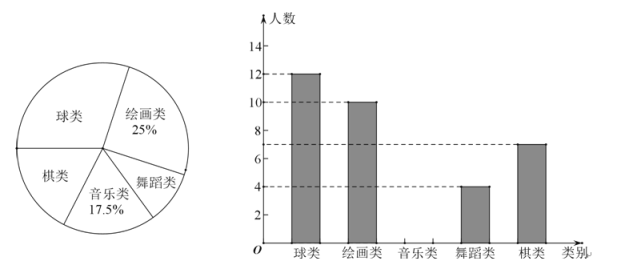
(1)参加音乐类活动的学生人数为 人,参加球类活动的人数的百分比为 ;
(2)该校学生共600人,则参加棋类活动的人数约为 ;
(3)该班参加舞蹈类活动的四位同学中,有一位男生(用E表示)和3位女生(分别用F,G,H表示),先准备从中选取两名同学组成舞伴,请用列表或画树状图得方法求恰好选中一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线y=ax2+bx+3=0(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C
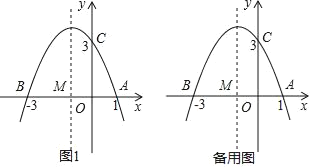
(1)求抛物线的解析式;
(2)设抛物线的对称轴与x轴交于点M,请问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由;
(3)在抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
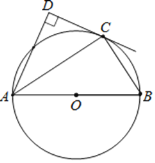
【题目】如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D.
(1)求证:AC平分∠DAB;
(2)求证:AC2=ADAB;
(3)若AD=![]() ,sinB=
,sinB=![]() ,求线段BC的长.
,求线段BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 中,
中,![]() ,
,![]() 的顶点
的顶点![]() 是底边
是底边![]() 的中点,两边分别与
的中点,两边分别与![]() 交于点
交于点![]() .
.
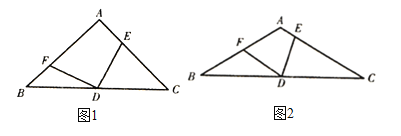
(1)如图1,![]() ,当
,当![]() 的位置变化时,
的位置变化时,![]() 是否随之变化?证明你的结论;
是否随之变化?证明你的结论;
(2)如图2,当![]() ,当
,当![]() °时,(1)中的结论仍然成立,求出此时
°时,(1)中的结论仍然成立,求出此时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级学生的理化实验操作情况,随机抽查了40名同学实验操作的得分.根据获取的样本数据,制作了如下的条形统计图和扇形统计图.请根据相关信息,解答下列问题:

(Ⅰ)扇形 ①的圆心角的大小是 ;
(Ⅱ)求这40个样本数据的平均数、众数、中位数;
(Ⅲ)若该校九年级共有320名学生,估计该校理化实验操作得满分(10分)有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,对角线AC与BD相交于点O,过点O作直线EF⊥BD,且交AC于点E,交BC于点F,连接BE、DF,且BE平分∠ABD.
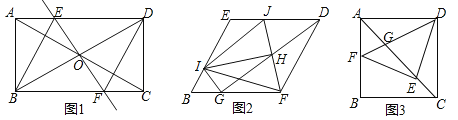
(1)①求证:四边形BFDE是菱形;②求∠EBF的度数.
(2)把(1)中菱形BFDE进行分离研究,如图2,G,I分别在BF,BE边上,且BG=BI,连接GD,H为GD的中点,连接FH,并延长FH交ED于点J,连接IJ,IH,IF,IG.试探究线段IH与FH之间满足的数量关系,并说明理由;
(3)把(1)中矩形ABCD进行特殊化探究,如图3,矩形ABCD满足AB=AD时,点E是对角线AC上一点,连接DE,作EF⊥DE,垂足为点E,交AB于点F,连接DF,交AC于点G.请直接写出线段AG,GE,EC三者之间满足的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有120间标准房,当每间标准房每天价格为100元时,每天都客满,市场调查表明每间标准房每天价格在100~180元之间(含100元,180元)浮动时,每提高5元,日均入住数减少3间,每间标准房如果有人入住每天各种费用40元,如果没人入住每天需各种费用10元,宾馆将每间标准房每天价格提高到多少元时,客房的日收益额最大?(注:收益额![]() 营业收入
营业收入![]() 各种费用)
各种费用)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com