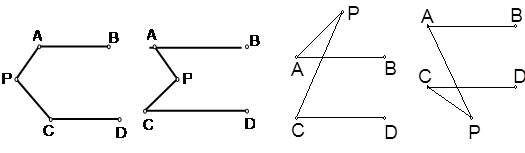试题分析:①首先过点P作PQ∥AB,又由AB∥CD,可得PQ∥AB∥CD,根据两直线平行,同旁内角互补,即可求得∠PBA+∠1=180°,∠2+∠PCD=180°,则可得∠APC+∠PAB+∠PCD=∠PBA+∠1+∠2+∠PCD=360°;
②首先过点P作PQ∥AB,又由AB∥CD,可得PQ∥AB∥CD,根据两直线平行,内错角相等,即可得∠1=∠PAB,∠2=∠PCD,则可得∠APC=∠PAB+∠PCD;
③由AB∥CD,根据两直线平行,同位角相等,即可得∠1=∠PCD,然后由三角形外角的性质,即可求得∠PCD=∠PAB+∠APC;
④由AB∥CD,根据两直线平行,内错角相等,即可得∠1=∠PAB,然后由三角形外角的性质,即可求得∠PAB=∠PCD+∠APC.
试题解析:如图:

①过点P作PQ∥AB,
∵AB∥CD,
∴PQ∥AB∥CD,
∴∠PAB+∠1=180°,∠2+∠PCD=180°,
∵∠APC=∠1+∠2,
∴∠APC+∠PAB+∠PCD=∠PAB+∠1+∠2+∠PCD=360°;
②过点P作PQ∥AB,
∵AB∥CD,
∴PQ∥AB∥CD,
∴∠1=∠PAB,∠2=∠PCD,
∵∠APC=∠1+∠2=∠PAB+∠PCD,
∴∠APC=∠PAB+∠PCD;
③∵AB∥CD,
∴∠1=∠PCD,
∵∠1=∠PAB+∠APC,
∴∠PCD=∠PAB+∠APC;
④∵AB∥CD,
∴∠1=∠PAB,
∵∠1=∠PCD+∠APC,
∴∠PAB=∠PCD+∠APC.