
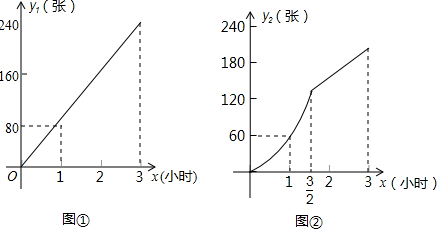
分析 (1)设函数的解析式为y=ax2,然后把点(1,60)代入解析式求得a的值,即可得出抛物线的表达式,根据图象可得自变量x的取值范围;
(2)设需要开放x个普通售票窗口,根据售出车票不少于350,列出不等式解不等式,求最小整数解即可;
(3)先求出普通窗口的函数解析式,然后求出8点时售出的票数,和无人售票窗口当x=$\frac{3}{2}$时,y的值,然后把运用待定系数法求解析式即可.
解答 解:(1)设函数的解析式为y=ax2,
把点(1,60)代入解析式得:a=60,
则函数解析式为:y=60x2(0≤x≤$\frac{3}{2}$);
故答案为:y=60x2,0≤x≤$\frac{3}{2}$.
(2)设需要开放x个普通售票窗口,
由题意得,80x+60×2≥350,
解得:x≥2$\frac{7}{8}$,
∵x为整数且x取最小值,
∴x=3,
即至少需要开放3个普通售票窗口;
(3)设普通售票的函数解析式为y=kx,
把点(1,80)代入得:k=80,
则y=80x,
∵8点是x=2,
∴当x=2时,y=160,
即上午8点普通窗口售票为160张,
由(1)得,当x=$\frac{3}{2}$时,y=135,
∴图②中的一次函数过点($\frac{3}{2}$,135),(2,160),
设一次函数的解析式为:y=mx+n,
把点的坐标代入得:$\left\{\begin{array}{l}{\frac{3}{2}m+n=135}\\{2m+n=160}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=50}\\{n=60}\end{array}\right.$,
则一次函数的解析式为y=50x+60.
点评 本题考查了二次函数及一次函数的应用,解答本题的关键是根据题意找出等量关系求出函数解析式,培养学生的读图能力以及把生活中的实际问题转化为数学问题来解决.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 姓名 | A | B | C | D | E | F | G | H | I |
| 成绩(米) | 0.91 | 0.95 | 1.10 | 0.98 | 1.08 | 0.96 | 1.12 | 1.18 | 1.17 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,等腰Rt△ABC的直角顶点在y轴上,斜边BC在x轴上,AB=AC=4$\sqrt{2}$,D为斜边BC的中点,点P由点A出发沿线段AB做匀速运动,P′是点P关于AD的对称点,P′P交y轴于点F,点Q由点D出发沿射线DC方向做匀速运动,且满足四边形QDPP′是平行四边形,设?QDPP′的面积为S,DQ=x.
如图,在平面直角坐标系中,等腰Rt△ABC的直角顶点在y轴上,斜边BC在x轴上,AB=AC=4$\sqrt{2}$,D为斜边BC的中点,点P由点A出发沿线段AB做匀速运动,P′是点P关于AD的对称点,P′P交y轴于点F,点Q由点D出发沿射线DC方向做匀速运动,且满足四边形QDPP′是平行四边形,设?QDPP′的面积为S,DQ=x.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
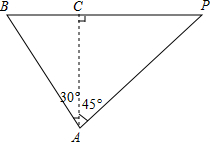 如图,一艘轮船原在A处,它的北偏东45方向上有一灯塔P,轮船沿着北偏西30方向航行4小时到达B处,这时灯塔P正好在轮船的正东方向上,已知轮船的速度为25海里/时.求轮船在B处时与灯塔P的距离(结果保留根号).
如图,一艘轮船原在A处,它的北偏东45方向上有一灯塔P,轮船沿着北偏西30方向航行4小时到达B处,这时灯塔P正好在轮船的正东方向上,已知轮船的速度为25海里/时.求轮船在B处时与灯塔P的距离(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
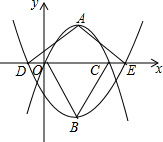 如图,在平面直角坐标系中,抛物线y=a1(x-2)2+2与y=a2(x-2)2-3的顶点分别为A,B,与x轴分别交于点O,C,D,E.若点D的坐标为(-1,0),则△ADE与△BOC的面积比为1.
如图,在平面直角坐标系中,抛物线y=a1(x-2)2+2与y=a2(x-2)2-3的顶点分别为A,B,与x轴分别交于点O,C,D,E.若点D的坐标为(-1,0),则△ADE与△BOC的面积比为1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com