
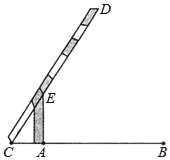
【题目】如图,小明在研究性学习活动中,对自己家所在的小区进行调查后发现,小区汽车入口宽AB为3.3m,在入口的一侧安装了停止杆CD,其中AE为支架.当停止杆仰起并与地面成60°角时,停止杆的端点C恰好与地面接触.此时CA为0.7m.在此状态下,若一辆货车高3m,宽2.5m,入口两侧不能通车,那么这辆货车在不碰杆的情况下,能从入口内通过吗?请你通过计算说明.(参考数据:![]() ≈1.7)
≈1.7)
 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】若关于x的不等式x﹣ ![]() <1的解集为x<1,则关于x的一元二次方程x2+ax+1=0根的情况是( )
<1的解集为x<1,则关于x的一元二次方程x2+ax+1=0根的情况是( )
A.有两个相等的实数根
B.有两个不相等的实数根
C.无实数根
D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是一个长为![]() 、宽为
、宽为![]() 的长方形,沿图中虛线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形.
的长方形,沿图中虛线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形.
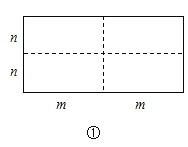
(1)图②中的阴影部分的面积为
(2)观察图②,请你写出代数式![]() 与
与![]() 之间的等量关系式
之间的等量关系式

(3)若![]() 则
则![]()
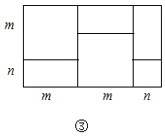
(4)实际上有许多代数恒等式可以用图形的面积来表示.如图③,它表示
(5)试画出一个几何图形,使它的面积能表示![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xoy中,一次函数y= ![]() x+3的图象与x轴和y轴交于A、B两点,将△AOB绕点O顺时针旋转90°后得到△A′OB′.
x+3的图象与x轴和y轴交于A、B两点,将△AOB绕点O顺时针旋转90°后得到△A′OB′.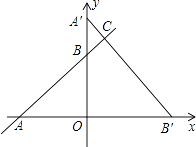
(1)求直线A′B′的解析式;
(2)若直线A′B′与直线AB相交于点C,求S△ABC:S△ABO的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点P,根据下列条件,求∠BPC的度数.
(1)若∠ABC=50°,∠ACB=60°,则∠BPC= ;
(2)若∠ABC+∠ACB=120°,则∠BPC= ;
(3)若∠A=80°,则∠BPC= ;
(4)从以上的计算中,你能发现已知∠A,求∠BPC的公式是:∠BPC= (提示:用∠A表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,数轴上,O点与C点对应的数分别是0、60(单位:单位长度),将一根质地均匀的直尺AB放在数轴上(A在B的左边),若将直尺在数轴上水平移动,当A点移动到B点的位置时,B点与C点重合,当B点移动到A点的位置时,A点与O点重合.
(1)直尺的长为多少个单位长度(直接写答案)
(2)如图2,直尺AB在数轴上移动,有BC=4OA,求此时A点对应的数;
(3)如图3,以OC为边搭一个横截面为长方形的不透明的篷子,将直尺放入篷内的数轴上的某处(看不到直尺的任何部分,A在B的左边),将直尺AB沿数轴以5个单位/秒的速度分别向左、向右移动,直到完全看到直尺,所经历的时间为t1、t2, 若t1﹣t2=2(秒),求直尺放入蓬内,A点对应的数为多少?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线AM∥BN,点E,F,D在射线AM上,点C在射线BN上,且∠BCD=∠A,BE平分∠ABF,BD平分∠FBC.
(1)求证:AB∥CD.
(2)如果平行移动CD,那么∠AFB与∠ADB的比值是否发生变化?若变化,找出变化规律;若不变,求出这两个角的比值.
(3)如果∠A=100°,那么在平行移动CD的过程中,是否存在某一时刻,使∠AEB=∠BDC?若存在,求出此时∠AEB的度数;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:
①四边形CFHE是菱形;
②EC平分∠DCH;
③线段BF的取值范围为3≤BF≤4;
④当点H与点A重合时,EF=2 ![]() .
.
以上结论中,你认为正确的有 . (填序号)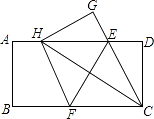
查看答案和解析>>
科目:初中数学 来源: 题型:
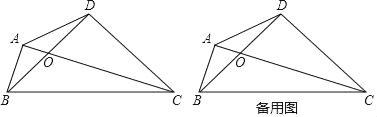
【题目】如图,四边形ABCD的对角线AC,BD相交于点O,OB=OD,BD=CD,∠BAC=∠BDC=90°.
(1)填空:∠ABD=∠ ;
(2)求![]() 的值;
的值;
(3)点D关于直线BC的对称点为N,连接AN,请补全图形,探究线段AN,AD有怎样的关系,并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com