
 (1)用适当的方法解下列一元二次方程:x2-6x+1=0.
(1)用适当的方法解下列一元二次方程:x2-6x+1=0.分析 (1)用配方法解一元二次方程,首先将常数项移到等号的右侧,将等号左右两边同时加上一次项系数一半的平方,即可将等号左边的代数式写成完全平方形式.
(2)根据矩形对角线的性质,矩形对角线互相平分且相等,可知EO=FO,BO=CO,∠BOE=∠COF,可知△BOE≌△COF,即可得出BE=CF.
解答 (1)解:x2-6x+1=0.
移项得,x2-6x=-1,
配方得,x2-6x+9=-1+9,
∴(x-3)2=8,
∴x-3=±2$\sqrt{2}$,
∴x1=3+2$\sqrt{2}$,x2=3-2$\sqrt{2}$.
(2)证明:∵矩形ABCD的对角线为AC和BD,
∴AO=CO=BO=DO,
∵E、F分别是矩形ABCD的对角线AC和BD上的点,AE=DF,
∴EO=FO,
在△BOE和△COF中,$\left\{\begin{array}{l}{EO=FO}&{\;}\\{∠EOB=∠FOC}&{\;}\\{BO=CO}&{\;}\end{array}\right.$,
∴△BOE≌△COF(SAS),
∴BE=CF.
点评 本题考查了配方法解一元二次方程,矩形的性质,全等三角形的判定与性质;熟练掌握配方法解一元二次方程和矩形的性质,证明三角形全等是解决问题(2)的关键.


科目:初中数学 来源: 题型:解答题
| 每月用水量 | 单价 |
| 不超过5m3 | 3元/m3 |
| 超过5m3不超过10m3的部分 | 5元/m3 |
| 超过10m3的部分 | 8元/m3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,AB=AC,EB=EC,下列判定不正确的是( )
如图,在△ABC中,AB=AC,EB=EC,下列判定不正确的是( )| A. | △ABD≌△ACE | B. | △ABE≌△ACE | C. | △BDE≌△CDE | D. | △ABD≌△ACD |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在矩形OABC中,点C在x轴上,点A在y轴上,且OA,OC的长分别是一元二次方程x2-18x+80=0的两个根(OA<OC),点E在BC上,将△ABE沿AE折叠,使点B落在OC上.
如图,在矩形OABC中,点C在x轴上,点A在y轴上,且OA,OC的长分别是一元二次方程x2-18x+80=0的两个根(OA<OC),点E在BC上,将△ABE沿AE折叠,使点B落在OC上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知二次函数y=-x2+2x+m图象过点A(3,0),与y轴交于点B
如图,已知二次函数y=-x2+2x+m图象过点A(3,0),与y轴交于点B查看答案和解析>>
科目:初中数学 来源: 题型:解答题
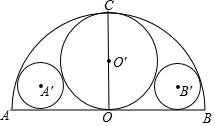 已知:如图,以AB为直径作半圆,半径OC⊥AB,以OC为直径作⊙OO′,再作⊙A′和⊙B都与AB、⊙O及⊙O′相切,如果AB=2R,求⊙A′的半径.
已知:如图,以AB为直径作半圆,半径OC⊥AB,以OC为直径作⊙OO′,再作⊙A′和⊙B都与AB、⊙O及⊙O′相切,如果AB=2R,求⊙A′的半径.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
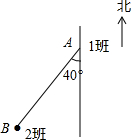 如图,在一次活动中,位于A处的1班准备前往相距5千米的B处与2班会合,请用方向和距离描述2班相对1班的位置:2班在1班的南偏西40°方向,距离A5千米的B处;反过来,请用方向和距离描述1班相对2班的位置:1班在2班的北偏东40°方向,距离B5千米的A处.
如图,在一次活动中,位于A处的1班准备前往相距5千米的B处与2班会合,请用方向和距离描述2班相对1班的位置:2班在1班的南偏西40°方向,距离A5千米的B处;反过来,请用方向和距离描述1班相对2班的位置:1班在2班的北偏东40°方向,距离B5千米的A处.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com