
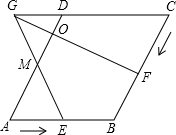
 ��ͼ������ABCD�ı߳�Ϊ6cm����DAB=60�㣬��M�DZ�AD�ϵ�һ�㣬��DM=2cm����E��F�ֱ��A��Cͬʱ��������1cm/s���ٶȷֱ��ر�AB��CB���B�˶���EM��CD���ӳ����ཻ��G��GF����O�����˶�ʱ��Ϊx��s������CGF�����Ϊy��cm2����
��ͼ������ABCD�ı߳�Ϊ6cm����DAB=60�㣬��M�DZ�AD�ϵ�һ�㣬��DM=2cm����E��F�ֱ��A��Cͬʱ��������1cm/s���ٶȷֱ��ر�AB��CB���B�˶���EM��CD���ӳ����ཻ��G��GF����O�����˶�ʱ��Ϊx��s������CGF�����Ϊy��cm2�������� ��1�����GF��AD����ôGF��BCҲ��ֱ���ɴ˿ɵó���CGF=30�㣬��CF=$\frac{1}{2}$GC������x��ʾ��CF��GC������GF��GC�ı�����ϵʽ�ɵó�����x�ķ��̣��������x��ֵ��
��2����F��FH��DC��H�㣬����y=$\frac{1}{2}$GC•FH���������������ε����ʺ����ҵĸ������GC��FH��ֵ���ɣ�
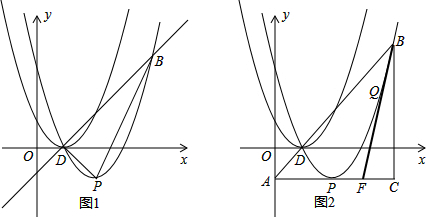
��3����D��DP��BC��P�������εĸ�PD=6��sin60��=$3\sqrt{3}$��������ε���������Ե�S����ODCF=$\frac{1}{6}$S����ʱ��ʹ���߶�GF������ABCD�ֳɵ��ϡ��������ֵ����֮��Ϊ5��7���������������ε����ʣ���x��ʾ�����ε����µ�OD��CF�����������ʽ�н������̶���⣮
��� �⣺��1����GF��AD��AD��BC
��GF��BC
�ߡ�C=60�㣬
���CGF=30��
��CF=$\frac{1}{2}$GC
��DM=2cm
��AM=4cm
�ߡ�DMG�ס�AME��
��$\frac{DG}{AE}=\frac{DM}{AM}$��
��$\frac{GD}{x}=\frac{2}{4}$��
��DG=$\frac{x}{2}$��
��GC=6+$\frac{x}{2}$��
��x=$\frac{1}{2}$��$\frac{1}{2}$x+6��
��x=4
�൱x=4ʱ��GF��AD��
��2���ߡ�DMG�ס�AME��
��$\frac{DG}{AE}=\frac{DM}{AM}$��
��DG=$\frac{DM•AE}{AM}=\frac{2x}{4}=\frac{x}{2}$��
��GC=6+$\frac{x}{2}$��
��F��FH��DC��H�㣬
��FH=CF•sin60��=$\frac{\sqrt{3}}{2}$��
��y=$\frac{1}{2}$GC•FH��
y=$\frac{1}{2}��6+\frac{x}{2}��•\frac{\sqrt{3}}{2}x=\frac{\sqrt{3}}{8}{x}^{2}+\frac{3\sqrt{3}}{2}x$��
��3�����˶�x��s��ʱ��GF�������ϡ��������ֵ������Ϊ5��7��
��ʱ��OGD�ס�FGC��
��$\frac{GD}{GC}=\frac{OD}{FC}$��
��$OD=\frac{GD•FC}{GC}=\frac{\frac{x}{2}•x}{6+\frac{x}{2}}=\frac{{x}^{2}}{x+12}$��
��D��DP��BC��P����PD=6��sin60��=$3\sqrt{3}$��
������֪��$\frac{1}{2}��\frac{{x}^{2}}{x+12}+x��•3\sqrt{3}=\frac{5}{12}��6��3\sqrt{3}$��
��$\frac{{x}^{2}}{x+12}+x=5$��
��ã�${x}_{1}=4��{x}_{2}=-\frac{15}{2}$����ȥ����
�����飺x=4��ԭ���̵Ľ⣮
�൱x=4ʱ��GF�������ϡ��������ֵ������Ϊ5��7��
���� ���⿼�������ε����ʣ�������Ǻ����ĸ�����������ε��ж������ʣ�һԪһ�η��̵Ľⷨ�Լ�����ϵ���������Ľ���ʽ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ACB�У���ACB=90�㣬CD��AB�����ԡ�AΪ�ڽǵ��������С�CAD����CAB��
��ͼ���ڡ�ACB�У���ACB=90�㣬CD��AB�����ԡ�AΪ�ڽǵ��������С�CAD����CAB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ�����������Ӹۿ�Aͬʱ�������״���16����/ʱ�ٶ��ر�ƫ��40�㷽���У��Ҵ�����ƫ��50�㷽���У�3Сʱ�״�����C�����Ҵ�����B������C��B�������60����ʣ��Ҵ��ĺ����Ƕ��٣�
��ͼ�����������Ӹۿ�Aͬʱ�������״���16����/ʱ�ٶ��ر�ƫ��40�㷽���У��Ҵ�����ƫ��50�㷽���У�3Сʱ�״�����C�����Ҵ�����B������C��B�������60����ʣ��Ҵ��ĺ����Ƕ��٣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2 | B�� | 1 | C�� | 0 | D�� | 7 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com