练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．在△ABC中，三边之比BC：AC：AB=1：$\sqrt{3}$：2，求cosA+tanA的值？

    分析 根据三边之比设出其中的一条边长，然后表示出另外两边的长，然后利用锐角三角函数的定义求值即可．

    解答 解：设BC=x，
    ∵BC：AC：AB=1：$\sqrt{3}$：2，
    ∴AC=$\sqrt{3}$x，AB=2x，
    ∵x2+（$\sqrt{3}$x）2=4x2=（2x）2，
    ∴∠C=90°，
    ∴cosA+tanA=$\frac{AC}{AB}$+$\frac{BC}{AC}$=$\frac{\sqrt{3}x}{2x}+\frac{x}{\sqrt{3}x}$=$\frac{5\sqrt{3}}{6}$．

    点评 本题考查了解直角三角形的知识，解题的关键是能够判定三角形是直角三角形，并正确的运用锐角三角函数的定义列式计算，难度不大．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    7．如图，△ABC中，点D在BC边上，有下列三个关系式：
    ①∠BAC=90°，②$\frac{BD}{AD}$=$\frac{AD}{DC}$，③AD⊥BC．
    选择其中两个式子作为已知，余下的一个作为结论，写出已知，求证，并证明．
    已知：
    求证：
    证明：

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．（1）计算：（$\sqrt{24}$-$\sqrt{2}$）-（$\sqrt{8}$+$\sqrt{6}$）；
    （2）因式分解：x2-3x-18．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，A，E，C，F在同一条直线上，AB=FD，BC=DE，AE=FC．求证：∠B=∠D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．某自行车厂计划平均每天生产200辆，但是由于种种原因，实际每天生产量与计划量相比有出入．表是某周的生产情况（超产记为正，减产记为负）：
    星期一二三四五六日
    增减+6-3-8+14-10+15-4
    （1）根据记录的数据可知该厂星期三生产自行车多少辆？
    （2）产量最多的一天比产量最少的一天多生产自行车多少辆？
    （3）根据记录的数据可知该厂本周实际共生产自行车多少辆？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．化简：
    （1）$\sqrt{1{2}^{2}+2{4}^{2}}$；
    （2）$\sqrt{8.1×1{0}^{4}}$；
    （3）$\sqrt{（\frac{8}{13}）^{2}-（\frac{2}{13}）^{2}}$；
    （4）$\sqrt{1\frac{1}{80}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图，AB∥CD，MG平分∠AGF，NH平分∠EHD，那么GM∥HN，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．如图，A在DE上，F在AB上，且AC=CE，∠1=∠2=∠3，则DE的长等于AB（请用图形中的线段表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

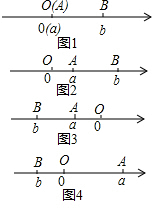    11．（1）阅读下面材料：点A、B在数轴上分别表示实数a、b，A、B两点之间的距离表示为|AB|．当A、B两点中有一点在原点时，不妨设点A在原点，如图1，|AB|=|OB|=|b|=|a-b|，当A、B两点都不在原点时，
    ①如图2，点A、B都在原点的右边，|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|；
    ②如图3，点A、B都在原点的左边，|AB|=|OB|-|OA|=|b|-|a|=（-b）-（-a）=a-b=|a-b|；
    ③如图4，点A、B在原点的两边，|AB|=|OB|+|OA|=|b|+|a|=（-b）+a=a-b=|a-b|；
    综上，数轴上A、B两点之间的距离|AB|=|a-b|．
    （2）回答下列问题：
    ①数轴上表示1005和-1011的两点之间的距离是2016；
    ②数轴上分别表示x、-5的两点A、B之间的距离是|x+5|，如果|AB|=2，那么x为-3或-7；
    ③若|x+3|＞|x-5|，则相应x的取值范围是x＞1；
    ④代数式|x+2|+|x-3|+|x-1|的最小值为5．

    查看答案和解析>>

    同步练习册答案