
【题目】在正方形ABCD中,AB=8,点P在边CD上,tan∠PBC=![]() ,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
(1)如图1,当点R与点D重合时,求PQ的长;
(2)如图2,试探索: ![]() 的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
(3)如图3,若点Q在线段BP上,设PQ=x,RM=y,求y关于x的函数关系式,并写出它的定义域.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;0≤x≤
;0≤x≤![]() .
.
【解析】试题分析:(1)由正方形的性质及![]() 可求出BC=8,PC=6,由勾股定理可求出BP=10,再由△
可求出BC=8,PC=6,由勾股定理可求出BP=10,再由△![]() ∽△
∽△![]() 即可求出结论;
即可求出结论;
(2)由正方形的性质得∠A=∠ABC=∠C=90°,由MQ∥AB得∠QMR=∠A,故∠QMR=∠C;由MQ∥AB得![]() ,而∠1+∠RQM=90°,∠ABP+∠PBC=90°,故
,而∠1+∠RQM=90°,∠ABP+∠PBC=90°,故![]() ,从而△
,从而△![]() ∽△
∽△![]() .故可得出结论;
.故可得出结论;
(3)延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,通过证明
,通过证明![]() ,分别计算
,分别计算![]() 及
及![]() ,
, ![]() ,从而可得出结论.
,从而可得出结论.
试题解析:(1)由题意,得![]() ,
,![]()
在Rt△![]() 中,
中, ![]()
∴![]()
∵![]()
∴![]() ∴
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
∵![]()
∴△![]() ∽△
∽△![]()
∴![]()
∴![]()
∴![]()
(2)答: ![]() 的比值随点
的比值随点![]() 的运动没有变化
的运动没有变化
理由:如图,
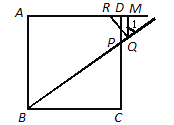
∵![]() ∥
∥![]()
∴![]() ,
, ![]()
∵![]()
∴![]()
∵![]()
∴![]()
![]()
∴![]()
∴△![]() ∽△
∽△![]()
∴![]()
∵![]() ,
, ![]()
∴![]()
∴![]() 的比值随点
的比值随点![]() 的运动没有变化,比值为
的运动没有变化,比值为![]()
(3)延长![]() 交
交![]() 的延长线于点
的延长线于点![]()
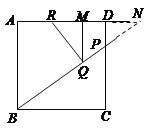
∵![]() ∥
∥![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∵![]() ∥
∥![]() ,
, ![]() ∥
∥![]()
∴![]() ∥
∥![]()
∴![]()
∵![]() ,
, ![]()
∴![]()
又![]() ,
, ![]()
∴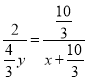
∴![]()
它的定义域是![]()


科目:初中数学 来源: 题型:
【题目】某校研究性学习小组在研究有关二次函数及其图象性质的问题时,发现了两个重要结论.一是发现抛物线y=ax2+2x+3(a≠0),当实数a变化时,它的顶点都在某条直线上;二是发现当实数a变化时,若把抛物线y=ax2+2x+3的顶点的横坐标减少![]() ,纵坐标增加
,纵坐标增加![]() ,得到A点的坐标;若把顶点的横坐标增加
,得到A点的坐标;若把顶点的横坐标增加![]() ,纵坐标增加
,纵坐标增加![]() ,得到B点的坐标,则A、B两点一定仍在抛物线y=ax2+2x+3上.
,得到B点的坐标,则A、B两点一定仍在抛物线y=ax2+2x+3上.
(1)请你协助探求出当实数a变化时,抛物线y=ax2+2x+3的顶点所在直线的解析式;
(2)问题(1)中的直线上有一个点不是该抛物线的顶点,你能找出它来吗?并说明理由;
(3)在他们第二个发现的启发下,运用“一般﹣一特殊﹣一般”的思想,你还能发现什么?你能用数学语言将你的猜想表述出来吗?你的猜想能成立吗?若能成立请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中.直线y=﹣x+3与x轴交于点B,与y轴交于点C,抛物线y=ax2+bx+c经过B,C两点,与x轴负半轴交于点A,连结AC,A(-1,0)
(1)求抛物线的解析式;
(2)点P(m,n)是抛物线上在第一象限内的一点,求四边形OCPB面积S关于m的函数表达式及S的最大值;
(3)若M为抛物线的顶点,点Q在直线BC上,点N在直线BM上,Q,M,N三点构成以MN为底边的等腰直角三角形,求点N的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图点P是△ABC的边BC上的一动点,点E与点P关于直线AB成轴对称,连接EP交AB于点F,连接AP、EC相交于点O,连接AE.

(1)判断AE与AP的数量关系,并说明理由.
(2)在点P的运动过程中,当AE∥BC时,判断AP与BP的数量关系,并说明理由.
(3)若∠BAC=900,点P在运动过程中是否存在线段AP与线段EC互相平分的情况,若存在,请求出点P的位置;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1 500 m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F.若小敏行走的路程为3 100 m,则小聪行走的路程为 m.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个少年在绿茵场上游戏.小红从点A出发沿线段AB运动到点B,小兰从点C出发,以相同的速度沿⊙O逆时针运动一周回到点C,两人的运动路线如图1所示,其中AC![]() DB.两人同时开始运动,直到都停止运动时游戏结束,其间他们与点C的距离y与时间x(单位:秒)的对应关系如图2所示.则下列说法正确的是( )
DB.两人同时开始运动,直到都停止运动时游戏结束,其间他们与点C的距离y与时间x(单位:秒)的对应关系如图2所示.则下列说法正确的是( )


A. 小红的运动路程比小兰的长
B. 两人分别在1.09秒和7.49秒的时刻相遇
C. 当小红运动到点D的时候,小兰已经经过了点D
D. 在4.84秒时,两人的距离正好等于⊙O的半径
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画图,探究:
(1)一个正方体组合图形的主视图、左视图(如图1)所示.
①这个几何体可能是(图2)甲、乙中的 ;
②这个几何体最多可由 个小正方体构成,请在图3中画出符合最多情况的一个俯视图.
(2)如图,已知一平面内的四个点A、B、C、D,根据要求用直尺画图.
①画线段AB,射线AD;
②找一点M,使M点即在射线AD上,又在直线BC上;
③找一点N,使N到A、B、C、D四个点的距离和最短.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 分别与x轴、y轴交于
分别与x轴、y轴交于![]() 两点,与直线
两点,与直线![]() 交于点C(4,2).
交于点C(4,2).
(1)点A坐标为( , ),B为( , );
(2)在线段![]() 上有一点E,过点E作y轴的平行线交直线
上有一点E,过点E作y轴的平行线交直线![]() 于点F,设点E的横坐标为m,当m为何值时,四边形
于点F,设点E的横坐标为m,当m为何值时,四边形![]() 是平行四边形;
是平行四边形;
(3)若点P为x轴上一点,则在平面直角坐标系中是否存在一点Q,使得![]() 四个点能构成一个菱形.若存在,求出所有符合条件的Q点坐标;若不存在,请说明理由.
四个点能构成一个菱形.若存在,求出所有符合条件的Q点坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图,不写作法,但要求保留作图痕迹.

(1)已知:线段a和∠α,如图.求作:△ABC,使得AB=a,∠ABC=∠α.∠BAC=2∠α.
(2)在(1)的条件下,若∠ABC=360,求∠ACB的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com