
【题目】如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于E,连接CE. 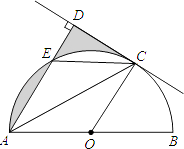
(1)判断CD与⊙O的位置关系,并证明你的结论;
(2)若E是 ![]() 的中点,⊙O的半径为1,求图中阴影部分的面积.
的中点,⊙O的半径为1,求图中阴影部分的面积.
【答案】
(1)解:CD与圆O相切.理由如下:
∵AC为∠DAB的平分线,
∴∠DAC=∠BAC,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠DAC=∠OCA,
∴OC∥AD,
∵AD⊥CD,
∴OC⊥CD,
则CD与圆O相切
(2)解:连接EB,交OC于F,
∵E为 ![]() 的中点,
的中点,
∴ ![]() ,
,
∴AE=EC,
∴∠EAC=∠ECA,
又∵∠EAC=∠OAC,
∴∠ECA=∠OAC,
∴CE∥OA,
又∵OC∥AD,
∴四边形AOCE是平行四边形,
∴CE=OA,AE=OC,
又∵OA=OC=1,
∴四边形AOCE是菱形,
∵AB为直径,得到∠AEB=90°,
∴EB∥CD,
∵CD与⊙O相切,C为切点,
∴OC⊥CD,
∴OC∥AD,
∵点O为AB的中点,
∴OF为△ABE的中位线,
∴OF= ![]() AE=
AE= ![]() ,即CF=DE=
,即CF=DE= ![]() ,
,
在Rt△OBF中,根据勾股定理得:EF=FB=DC= ![]() ,
,
则S阴影=S△DEC= ![]() ×
× ![]() ×
× ![]() =
= ![]() .
.

【解析】(1)CD与圆O相切,理由为:由AC为角平分线得到一对角相等,再由OA=OC,利用等边对等角得到一对角相等,等量代换得到一对内错角相等,利用内错角相等两直线平行得到OC与AD平行,根据AD垂直于CD,得到OC垂直于CD,即可得证;(2)根据E为弧AC的中点,得到弧AE=弧EC,利用等弧对等弦得到AE=EC,可得出弓形AE与弓形EC面积相等,阴影部分面积拼接为直角三角形DEC的面积,求出即可.


科目:初中数学 来源: 题型:
【题目】爸爸开车带着小明在公路上匀速行驶,小明每隔一段时间看到的里程碑上的数如下
时刻 | 9:00 | 9:45 | 12:00 |
碑上的数 | 是一个两位数,数字之和是9 | 十位与个位数字与9:00时所看到的正好相反 | 比9:00时看到的两位数中间多了个0 |
9:00时看到的两位数是( )
A. 54 B. 45 C. 36 D. 27
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底点G为BC的中点,则矮建筑物的高CD为( )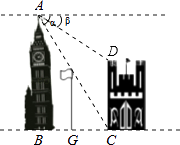
A.20米
B.10 ![]() 米
米
C.15 ![]() 米
米
D.5 ![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用直尺和圆规画一个角等于已知角,是运用了“全等三角形的对应角相等”这一性质,其全等的依据是( )
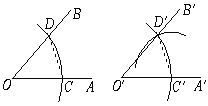
A.SAS B.ASA C.AAS D.SSS
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=x+1的图象与反比例函数 ![]() (k为常数,且k≠0)的图象都经过点A(m,2)
(k为常数,且k≠0)的图象都经过点A(m,2) 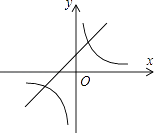
(1)求点A的坐标及反比例函数的表达式;
(2)结合图象直接比较:当x>0时,y1和y2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB=20cm,CD=2cm,线段CD在线段AB上运动,E、F分别是AC、BD的中点.
(1)若AC=4cm,则EF=_______cm.
(2)当线段CD在线段AB上运动时,EF的长度是否改变,如果变化,请说明理由.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com