
如图,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连结BG,DE.我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系:
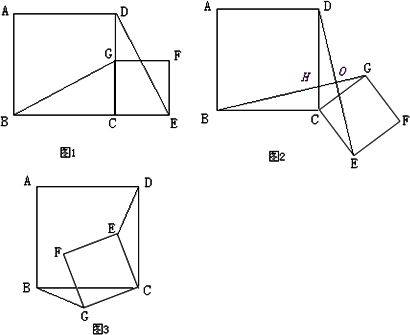
(1)①猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系;
②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度,得到如图2、如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判
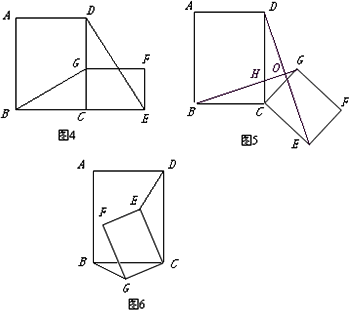
(2)将原题中正方形改为矩形(如图图6),且AB=a,BC=b,CE=ka,CG=kb(a≠b,k>0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图5为例简要说明理由.
(3)在第(2)题图5中,连结DG、BE,且a=3,b=2,k=![]() ,求BE2+DG2的值.
,求BE2+DG2的值.
|
(1)①BG=DE,BG⊥DE 1分 ②BG=DE,BG⊥DE仍然成立 2分 在图(2)中证明如下 ∵四边形ABCD、四边形ABCD都是正方形 ∴BC=CD,CG=CE,∠BCD=∠ECG=90° ∴∠BCG=∠DCE ∴△BCG≌△DCE(SAS) 3分 ∴BG=DE ∠CBG=∠CDE 又∵∠CBG+∠BHC=90° ∠BGC=∠DHO ∴∠CDE+∠DHO=90° ∴∠DOH=90° ∴BG⊥DE 4分 (2)BG⊥DE成立,BG=DE不成立 6分 简要说明如下 ∵四边形ABCD、四边形CEFG都是矩形, 且AB=a,BC=b,CG=kb,CE=ka(a≠b,k>0) ∴ ∴∠BCG=∠DCE ∴△BCG∽△DCE 7分 ∴∠CBG=∠CDE 又∵∠BHC=∠DHO ∠CBG+∠BHC=90° ∴∠CDE+∠DHO=90° ∴∠DOH=90° ∴BG⊥DE 8分 (3)∵BG⊥DE ∴BE2+DG2=OB2+OE2+OG2+OD2=BD2+GE2 又∵a=3,b=2,k= ∴BD2+GE2=22+32+12+( ∴BE2+DG2= |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
 如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条)
如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条)查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF.
如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com