
【题目】如图,已知:抛物线y=a(x+1)(x﹣3)与x轴相交于A、B两点,与y轴的交于点C(0,﹣3).
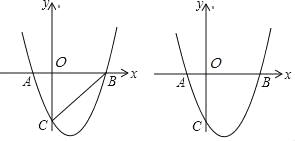
(1)求抛物线的解析式的一般式.
(2)若抛物线上有一点P,满足∠ACO=∠PCB,求P点坐标.
(3)直线l:y=kx﹣k+2与抛物线交于E、F两点,当点B到直线l的距离最大时,求△BEF的面积.
【答案】(1)y=x2﹣2x﹣3;(2)(4,5)或(![]() );(3)10
);(3)10
【解析】
(1)把C点坐标代入y=a(x+1)(x-3)中求出a的值即可得到抛物线解析式;
(2)分两种情况,当点P在直线BC的下方时,过点B作BE⊥BC交CP的延长线于点E,过点E作EM⊥x轴于点M,由直角三角形的性质可求得ME,BM长,求出点E的坐标,可求出直线CE的解析式,联立直线和抛物线方程可求出点P的坐标;当点P在直线BC的上方时,过点B作BF⊥BC交CP于点F,同理求出点F的坐标和直线CF的解析式,联立直线和抛物线方程可求得点P的坐标;
(3)求出直线y=kx-k+2恒过定点H(1,2),连结BH,当BH⊥直线l时,点B到直线l的距离最大时,求出此时k的值,可求出点E,F的坐标,则△BEF的面积可求出.
解:(1)把C(0,﹣3)代入y=a(x+1)(x﹣3),
得﹣3a=﹣3,解得a=1,
所以抛物线解析式为y=(x+1)(x﹣3),即y=x2﹣2x﹣3;
(2)当点P在直线BC的下方时,如图1,过点B作BE⊥BC交CP的延长线于点E,过点E作EM⊥x轴于点M,
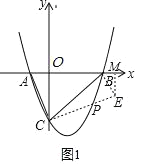
∵y=(x+1)(x﹣3),
∴y=0时,x=﹣1或x=3,
∴A(﹣1,0),B(3,0),
∴![]() ,
,
∵OB=OC=3,
∴∠ABC=45°,![]() ,
,
∵∠ACO=∠PCB,
∴![]() ,
,
∴![]() ,
,
∵∠CBE=90°,
∴∠MBE=45°,
∴BM=ME=1,
∴E(4,﹣1),
设直线CE的解析式为y=kx+b,
∴![]() ,
,
解得: ,
,
∴直线CE的解析式为![]() ,
,
∴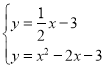 ,
,
解得![]() ,
,![]() ,
,
把![]() 代入
代入![]() 得
得![]() ,
,
∴![]() ,
,
当点P在直线BC的上方时,过点B作BF⊥BC交CP于点F,如图2,
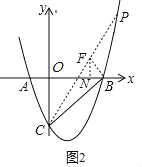
同理求出![]() ,FN=BN=1,
,FN=BN=1,
∴F(2,1),
求出直线CF的解析式为y=2x﹣3,
∴ ,
,
解得:x1=0,x2=4,
∴P(4,5).
综合以上可得点P的坐标为(4,5)或(![]() );
);
(3)∵直线l:y=kx﹣k+2,
∴y﹣2=k(x﹣1),
∴x﹣1=0,y﹣2=0,
∴直线y=kx﹣k+2恒过定点H(1,2),如图3,连结BH,当BH⊥直线l时,点B到直线l的距离最大时,
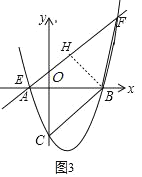
求出直线BH的解析式为y=﹣x+3,
∴k=1,
∴直线l的解析式为y=x+1,
∴![]() ,
,
解得: ,
, ,
,
∴E(﹣1,0),F(4,5),
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+2ax+3a2+3(其中x是自变量),当x≥2时,y随x的增大而增大,且-2≤x≤1时,y的最大值为9,则a的值为![]()
![]()
A. 1或![]() B. -
B. -![]() 或
或![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中的两个图形M与N,给出如下定义:P为图形M上任意一点,Q为图形N上任意一点,如果P,Q两点间的距离有最小值,那么称这个最小值为图形M,N间的“和睦距离”,记作d(M,N).若图形M,N有公共点,则d(M,N)=0.
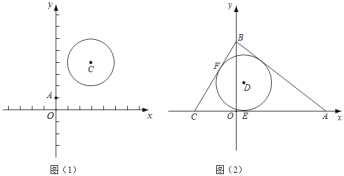
(1)如图,A(0,1),C(3,4),⊙C的半径为2,则d(C,⊙C)= ,d(O,⊙C)= ;
(2)已知,如图,△ABC的一边AC在x轴上,B在y轴上,且AC=8,AB=7,BC=5.
①D是△ABC内一点,若AC、BC分别切⊙D于E、F,且d(C,D)=2d(D,AB),判断AB与⊙D的位置关系,并求出D点的坐标;
②若以r为半径,①中的D为圆心的⊙D,有d(B,⊙D)>1,d(C,⊙D)<2,直接写出r的取值范围 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了计算湖中小岛上凉亭P到岸边公路l的距离,某数学兴趣小组在公路l上的点A处,测得凉亭P在北偏东60°的方向上;从A处向正东方向行走200米,到达公路l上的点B处,再次测得凉亭P在北偏东45°的方向上,如图所示.求凉亭P到公路l的距离.(结果保留整数,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
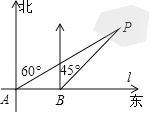
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD(四边相等、四内角相等)中,AD=5,点E、F是正方形ABCD内的两点,且AE=FC=4,BE=DF=3,则EF的平方为( )

A.2B.![]() C.3D.4
C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)是一款手机支架,忽略支管的粗细,得到它的简化结构图如图(2)所示.已知支架底部支架CD平行于水平面,EF⊥OE,GF⊥EF,支架可绕点O旋转,OE=20cm,EF=20![]() cm.如图(3)若将支架上部绕O点逆时针旋转,当点G落在直线CD上时,测量得∠EOG=65°.
cm.如图(3)若将支架上部绕O点逆时针旋转,当点G落在直线CD上时,测量得∠EOG=65°.
(1)求FG的长度(结果精确到0.1);
(2)将支架由图(3)转到图(4)的位置,若此时F、O两点所在的直线恰好于CD垂直,点F的运动路线的长度称为点F的路径长,求点F的路径长.
(参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14,1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段 AC=4,线段BC绕点C旋转,且BC=6,连结AB,以AB为边作正方形ADEB,连结CD.
(1)若∠ACB=90°,则AB的值是____;
(2)线段CD长的最大值是____.
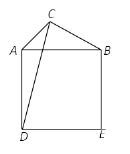
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题提出)如果从![]() ,
,![]() 个连续的自然数中选择
个连续的自然数中选择![]() 个连续的自然数
个连续的自然数![]() ,有多少种不同的选择方法?
,有多少种不同的选择方法?
(问题探究)为发现规律,我们采用一般问题特殊化的策略,先从最简单的问题入手,再逐次递进,最后得出一般性的结论.
探究一:如果从![]() ,
,![]() 个连续的自然数中选择
个连续的自然数中选择![]() 个连续的自然数,会有多少种不同的选择方法?
个连续的自然数,会有多少种不同的选择方法?
当![]() ,
,![]() 时,显然有
时,显然有![]() 种不同的选择方法;
种不同的选择方法;
![]()
当![]() ,
,![]() 时,有
时,有![]() ,
,![]() ;
;![]() ,
,![]() ;
;![]() ,
,![]() 这
这![]() 种不同的选择方法;
种不同的选择方法;
![]()
当![]() ,
,![]() 时,有________种不同的选择方法;
时,有________种不同的选择方法;

……
由上可知:从![]() 个连续的自然数中选择
个连续的自然数中选择![]() 个连续的自然数,有_______种不同的选择方法.
个连续的自然数,有_______种不同的选择方法.
探究二:如果从![]() ,
,![]() 个连续的自然数中选择
个连续的自然数中选择![]() 个,
个,![]() 个……
个……![]()
![]() 个连续的自然数,分别有多少种不同的选择方法?
个连续的自然数,分别有多少种不同的选择方法?
我们借助下面的框图继续探究,发现规律并应用规律完成填空.
|
|
| ... |
|
|
|
|
|
|
|
|
从![]() 个连续的自然数中选择
个连续的自然数中选择![]() 个连续的自然数,有_______种不同的选择方法;
个连续的自然数,有_______种不同的选择方法;
从![]() 个连续的自然数中选择
个连续的自然数中选择![]() 个连续的自然数,有_______种不同的选择方法;
个连续的自然数,有_______种不同的选择方法;
……
从![]() 个连续的自然数中选择
个连续的自然数中选择![]() 个连续的自然数,有_______种不同的选择方法;
个连续的自然数,有_______种不同的选择方法;
……
由上可知:如果从![]() ,
,![]() 个连续的自然数中选择
个连续的自然数中选择![]()
![]() 个连续的自然数,有______种不同的选择方法.
个连续的自然数,有______种不同的选择方法.
(问题解决)如果从![]() ,
,![]() 个连续的自然数中选择
个连续的自然数中选择![]() 个连续的自然数
个连续的自然数![]() ,有_______种不同的选择方法.
,有_______种不同的选择方法.
(实际应用)我们运用上面探究得到的结论,可以解决生活中的一些实际问题.
(1)今年国庆七天长假期间,小亮想参加某旅行社组织的青岛两日游,在出行日期上,他共有______种不同的选择.
(2)星期天,小明、小强和小华三个好朋友去电影院观看《我和我的祖国》,售票员李阿姨为他们提供了第七排![]() 号到
号到![]() 号的电影票让他们选择,如果他们想拿三张连号票,则一共有______种不同的选择方法.
号的电影票让他们选择,如果他们想拿三张连号票,则一共有______种不同的选择方法.
(拓展延伸)如图,将一个![]() 的图案放置在
的图案放置在![]() 的方格纸中,使它恰好盖住其中的四个小正方形,共有______种不同的放置方法.
的方格纸中,使它恰好盖住其中的四个小正方形,共有______种不同的放置方法.
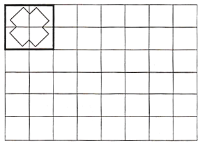
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 于点D,将
于点D,将![]() 绕点B顺时针旋转
绕点B顺时针旋转![]() 得到
得到![]()
![]() 如图2,当
如图2,当![]() 时,求点C、E之间的距离;
时,求点C、E之间的距离;
![]() 在旋转过程中,当点A、E、F三点共线时,求AF的长;
在旋转过程中,当点A、E、F三点共线时,求AF的长;
![]() 连结AF,记AF的中点为P,请直接写出线段CP长度的最小值.
连结AF,记AF的中点为P,请直接写出线段CP长度的最小值.
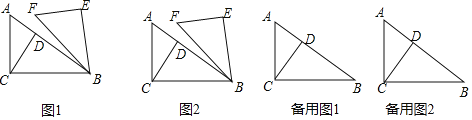
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com