
 如图是一个横断面为抛物线形状的拱桥,当水面宽4米时,拱顶(拱桥洞的最高点)离水面2米,水面上升1米时,水面的宽度为2$\sqrt{2}$米.
如图是一个横断面为抛物线形状的拱桥,当水面宽4米时,拱顶(拱桥洞的最高点)离水面2米,水面上升1米时,水面的宽度为2$\sqrt{2}$米. 分析 根据题意建立合适的平面直角坐标系,然后求出函数的解析式,然后令y=1求出相应的x的值,则水面的宽就是此时两个x的差的绝对值.
解答 解:如右图所示,建立平面直角坐标系,
设抛物线的解析式为:y=a(x-2)2+2,
∵函数图象过点(0,0),
∴0=a(0-2)2+2,得a=$-\frac{1}{2}$,
∴抛物线的解析式为:y=$-\frac{1}{2}(x-2)^{2}+2$,
当y=1时,1=$-\frac{1}{2}(x-2)^{2}+2$,
解得,${x}_{1}=2-\sqrt{2}$,${x}_{2}=2+\sqrt{2}$,
∴水面的宽度是:$(2+\sqrt{2})-(2-\sqrt{2})=2\sqrt{2}$,
故答案为:2$\sqrt{2}$.
点评 本题考查二次函数的应用,解答此类问题的关键是明确题意,求出相应的函数解析式,根据函数值求出相应的x的值.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
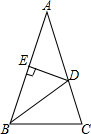 如图,在△ABC中,AB=AC,∠A=36°,BD为角平分线,DE⊥AB,垂足为E.
如图,在△ABC中,AB=AC,∠A=36°,BD为角平分线,DE⊥AB,垂足为E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
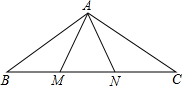 如图,△ABN≌△ACM,AB=AC,BN=CM,∠B=50°,∠ANB=60°,则∠MAC的度数等于( )
如图,△ABN≌△ACM,AB=AC,BN=CM,∠B=50°,∠ANB=60°,则∠MAC的度数等于( )| A. | 120° | B. | 70° | C. | 60° | D. | 50°. |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点A的坐标为(-$\sqrt{2}$,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为( )
如图,点A的坐标为(-$\sqrt{2}$,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为( )| A. | (0,0) | B. | (-1,-1) | C. | (-$\frac{1}{2}$,-$\frac{1}{2}$) | D. | (-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com