
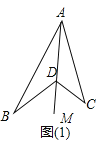
【题目】图(1)是我们常见的“箭头图”,其中隐藏着哪些数学知识呢?下面请你解决以下问题:

(1)观察如图(1)“箭头图”,试探究∠BDC与∠A、∠B、∠C之间大小的关系,并说明理由;
(2)请你直接利用以上结论,回答下列两个问题:
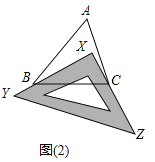
①如图(2),把一块三角板XYZ放置在△ABC上,使其两条直角边XY、XZ恰好经过点B、C.若∠A=50°,则∠ABX+∠ACX= ;
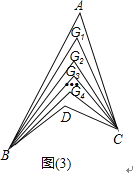
②如图(3),∠ABD,∠ACD的五等分线分别相交于点G1、G2、G3、G4,若∠BDC=135°,∠BG1C=67°,求∠A的度数.
【答案】(1)∠BDC=∠A+∠B+∠C(2)①40°②50°
【解析】试题分析:(1)连接AD并延长,根据三角形的外角和内角关系解答;
(2)①利用(1)的结论,直接计算出∠ABX+∠ACX的度数;
②图(3)利用(1)的结论,根据∠BDC=135°,∠BG1C=67°,计算出相等的角:∠DBG4+∠DCG4的和,再次利用(1)的结论,求出∠A的度数.
试题解析:(1)∠BDC=∠A+∠B+∠C.理由:
连接AD并延长到M.
因为∠BDM=∠BAD+∠B,∠CDM=∠CAD+∠C,
所以∠BDM+∠CDM=∠BAD+∠B+∠CAD+∠C,
即∠BDC=∠BAC+∠B+∠C.
(2)①由(1)知:∠BXC=∠A+∠ABX+∠ACX,
由于∠BXC=90°,∠A=50°
所以∠ABX+∠ACX
=∠BXC﹣∠A
=90°﹣50°
=40°.
②在箭头图G1BDC中
因为∠BDC=∠G1+∠G1BD+∠G1CD,
又∵∠BDC=135°,∠BG1C=67°
∵∠ABD,∠ACD的五等分线分别相交于点G1、G2、G3、G4
∴4(∠DBG4+∠DCG4)=135°﹣67°
∴∠DBG4+∠DCG4=17°.
∴∠ABG1+∠ACG1=17°
∵在箭头图G1BAC中
∵∠BG1C=∠A+∠G1BA+∠G1CA,
又∵∠BG1C=67°,
∴∠A=50°.
答:∠A的度数是50°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.
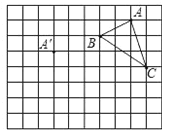
(1)请画出平移后的△A′B′C′,并求△A′B′C′的面积;
(2)若连接AA′,CC′,则这两条线段之间的关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
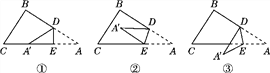
【题目】△ABC是一个三角形的纸片,点D,E分别是△ABC边AB,AC上的两点.
(1)如图①,如果沿直线DE折叠,则∠BDA′与∠A的关系是____________;
(2)如果折成图②的形状,猜想∠BDA′,∠CEA′和∠A的关系,并说明理由;
(3)如果折成图③的形状,猜想∠BDA′,∠CEA′和∠A的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
解答“已知![]() ,且
,且![]() ,
,![]() ,确定
,确定![]() 的取值范围”有如下解,
的取值范围”有如下解,
解:∵![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∴![]() .
.
又∵![]() ,
,
∴![]() ,
,![]() ①
①
同理得:![]() .
.![]() ②
②
由①![]() ②得
②得![]() .
.
∴![]() 的取值范围是
的取值范围是![]() .
.
请按照上述方法,完成下列问题:
(![]() )已知
)已知![]() ,且
,且![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
(![]() )已知
)已知![]() ,
,![]() ,若
,若![]() ,且
,且![]() ,求
,求![]() 得取值范围(结果用含
得取值范围(结果用含![]() 的式子表示).
的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B在反比例函数y=![]() 的图象上,过点A、B作x轴的垂线,垂足分别是M、N,射线AB交x轴于点C,若OM=MN=NC,四边形AMNB的面积是3,则k的值为( )
的图象上,过点A、B作x轴的垂线,垂足分别是M、N,射线AB交x轴于点C,若OM=MN=NC,四边形AMNB的面积是3,则k的值为( )
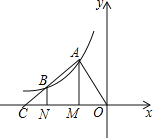
A.2 B.4 C.﹣2 D.﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
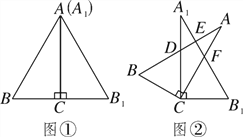
【题目】将两块相同的含30°角的直角三角板按图①的方式放置,已知∠BAC=∠B1A1C=30°,AB=2BC.固定三角板A1B1C,然后将三角板ABC绕点C顺时针方向旋转至图②的位置,AB与A1C、A1B1分别交于点D、E,AC与A1B1交于点F.
(1)当旋转角等于20°时,∠BCB1=________度;
(2)当旋转角等于多少度时,AB与A1B1垂直?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空:如图,已知∠B=∠CGF,∠DGF=∠F,求证∠B+∠F=180°.
证明:∵∠B= (已知),
∴AB∥C( ),
∵∠DGF= (已知),
∴CD∥EF( ),
∴AB∥ ( )
∴∠B+ =180°( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
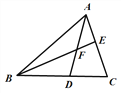
【题目】如图, ![]() ABC的中线AD、BE相交于点F,下列结论正确的有 ( )
ABC的中线AD、BE相交于点F,下列结论正确的有 ( )
①S△ABD=S△DCA;② S△AEF=S△BDF;③S四边形EFDC=2S△AEF;④S△ABC=3S△ABF
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=60°,BE⊥AC,垂足为E,CF⊥AB,垂足为F,点D是BC的中点,BE,CF交于点M.
(1)如果AB=AC,求证:△DEF是等边三角形;
(2)如果AB≠AC,试猜想△DEF是不是等边三角形?如果△DEF是等边三角形,请加以证明;如果△DEF不是等边三角形,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com