
【题目】(1)化简: ![]() (2)解方程:
(2)解方程:![]() .
.
【答案】(1) ![]() 或
或![]() ;(2)x=-2.
;(2)x=-2.
【解析】(1)先把括号内通分,再把除法转化为乘法,并把分子、分母分解因式约分化简;
(2)两边都乘以最简公分母2(x+3),把分式方程化为整式方程求解,求出x的值不要忘记检验.
(1)原式=![]() =
=![]() =
=![]() 或
或![]() ;
;
(2)解:去分母得:![]() ,
,
解得:x=﹣2,
经检验x=﹣2是分式方程的解,
∴原方程的解为x=﹣2
点睛:本题考查了分式的混合运算和解分式方程,熟练掌握分式的运算法则和解分式方程的方法是解答本题的关键.
【题型】解答题
【结束】
20
【题目】小张同学学完统计知识后,随机调查了她所在辖区若干名居民的年龄,将调查数据绘制成如下扇形统计图和条形统计图:

请根据以上不完整的统计图提供的信息,解答下列问题:
(1)小张同学共调查了 名居民的年龄,扇形统计图中a= ;
(2)补全条形统计图,并注明人数;
(3)若在该辖区中随机抽取一人,那么这个人年龄是60岁及以上的概率为 ;
(4)若该辖区年龄在0~14岁的居民约有2400人,请估计该辖区居民有多少人?
科目:初中数学 来源: 题型:
【题目】某商店第一次用500元购进钢笔若干支,第二次又用500元购进该款钢笔,但这次每支的进价是第一次进价的 ![]() 倍,购进数量比第一次少了25支.
倍,购进数量比第一次少了25支.
(1)求第一次每支钢笔的进价是多少元?
(2)若要求这两次购进的钢笔按同一价格全部销售完毕后获利不低于350元,问每支售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“在线教育”指的是通过应用信息科技和互联网技术进行内容传播和快速学习的方法.“互联网+”时代,中国的在线教育得到迅猛发展. 请根据下面张老师与记者的对话内容,求2014年到2016年中国在线教育市场产值的年平均增长率.
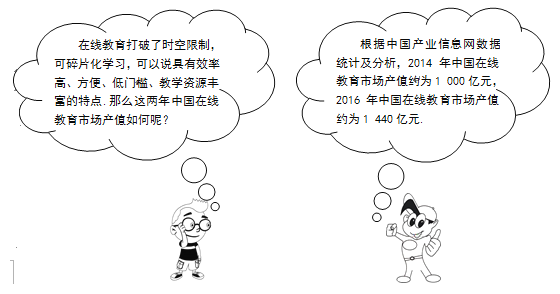
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校组建了书法、音乐、美术、舞蹈、演讲五个社团,全校每一名学生都参加且只参加了其中一个社团的活动.校团委从全校学生中随机选取部分学生进行了参加活动情况的调查,并将调查结果制成了如图不完整的统计图.请根据统计图完成下列问题:
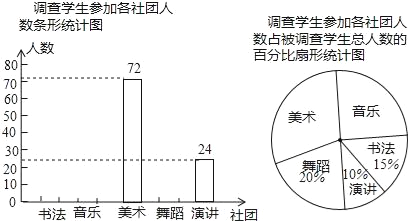
(1)参加本次调查有 名学生?
(2)根据调查数据分析,被调查的学生中有 名学生参加了音乐社团?
(3)请你补全条形统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面的变形规律:
![]() ;
;![]() ;
;![]() ;….
;….
解答下面的问题:
(1)仿照上面的格式请写出![]() = ;
= ;
(2)若n为正整数,请你猜想![]() = ;
= ;
(3)基础应用:计算:![]() .
.
(4)拓展应用1:解方程:![]() =2016
=2016
(5)拓展应用2:计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题
(1)求值:2 ![]() sin45°+(﹣3)2﹣20170×|﹣4|+
sin45°+(﹣3)2﹣20170×|﹣4|+ ![]() ;
;
(2)先化简,再求值:( ![]() ﹣x﹣1)÷
﹣x﹣1)÷ ![]() ,其中x是不等式组
,其中x是不等式组 ![]() 的一个整数解.
的一个整数解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系△ABC是格点三角形(顶点在网格线的交点上)
(1)先作△ABC关于原点O成中心对称的△A1B1C1,再把△A1B1C1向上平移4个单位长度得到△A2B2C2;
(2)△A2B2C2与△ABC是否关于某点成中心对称?若是,直接写出对称中心的坐标;若不是,请说明理由.
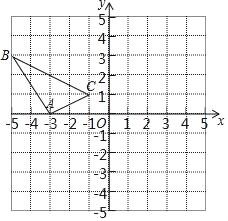
【答案】(1)画图见解析;(2)(0,2).
【解析】
(1)根据中心对称和平移性质分别作出变换后三顶点的对应点,再顺次连接可得;
(2)根据中心对称的概念即可判断.
(1)如图所示,△A1B1C1和△A2B2C2即为所求;
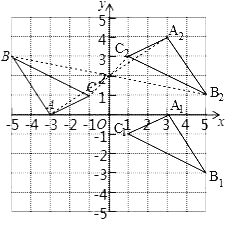
(2)由图可知,△A2B2C2与△ABC关于点(0,2)成中心对称.
点睛:本题考查了中心对称作图和平移作图,熟练掌握中心对称的性质和平移的性质是解答本题的关键. 中心对称的性质:①关于中心对称的两个图形能够完全重合;②关于中心对称的两个图形,对应点的连线都经过对称中心,并且被对称中心平分.
【题型】解答题
【结束】
22
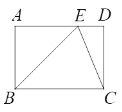
【题目】如图,在矩形ABCD中,点E在AD上,且EC平分∠BED.
(1)△BEC是否为等腰三角形?证明你的结论.
(2)已知AB=1,∠ABE=45°,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标中,点O为坐标原点,直线y=﹣x+4与x轴交于点A,过点A的抛物线y=ax2+bx与直线y=﹣x+4交于另一点B,且点B的横坐标为1.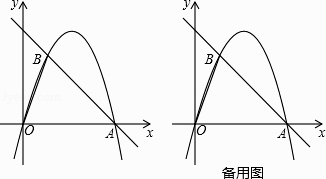
(1)求a,b的值;
(2)点P是线段AB上一动点(点P不与点A、B重合),过点P作PM//OB交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交AB于点N,过点P作PF⊥MC于点F,设PF的长为t,MN的长为d,求d与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,当S△ACN=S△PMN时,连接ON,点Q在线段BP上,过点Q作QR//MN交ON于点R,连接MQ、BR,当∠MQR﹣∠BRN=45°时,求点R的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=2,点E在边AD上,∠ABE=45°,BE=DE,连接BD,点P在线段DE上,过点P作PQ//BD交BE于点Q,连接QD.设PD=x,△PQD的面积为y,则能表示y与x函数关系的图象大致是( )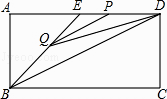
A.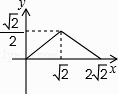
B.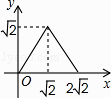
C.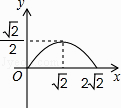
D.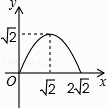
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com