
°ĺŐ‚ńŅ°Ņ»ÁÕľ1£¨‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ÷–£¨Ň◊őÔŌŖĺ≠Ļż◊ÝĪÍ‘≠Ķ„O£¨Ķ„A£®6£¨©Ā6 ![]() £©£¨«““‘y÷Šő™∂‘≥∆÷Š£ģ
£©£¨«““‘y÷Šő™∂‘≥∆÷Š£ģ
£®1£©«ůŇ◊őÔŌŖĶńĹ‚őŲ Ĺ£Ľ
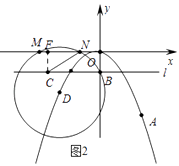
£®2£©»ÁÕľ2£¨ĻżĶ„B£®0£¨©Ā ![]() £©◊ųx÷ŠĶń∆Ĺ––ŌŖl£¨Ķ„C‘ŕ÷ĪŌŖl…Ō£¨Ķ„D‘ŕy÷Š◊ů≤ŗĶńŇ◊őÔŌŖ…Ō£¨Ń¨Ĺ”DB£¨“‘Ķ„Dő™‘≤–ń£¨“‘DBő™įŽĺ∂Ľ≠‘≤£¨°—D”Žx÷ŠŌŗĹĽ”ŕĶ„M£¨N£®Ķ„M‘ŕĶ„NĶń◊ů≤ŗ£©£¨Ń¨Ĺ”CN£¨ĶĪMN=CN Ī£¨«ů»ŮĹ«°ŌMNCĶń∂» ż£Ľ
£©◊ųx÷ŠĶń∆Ĺ––ŌŖl£¨Ķ„C‘ŕ÷ĪŌŖl…Ō£¨Ķ„D‘ŕy÷Š◊ů≤ŗĶńŇ◊őÔŌŖ…Ō£¨Ń¨Ĺ”DB£¨“‘Ķ„Dő™‘≤–ń£¨“‘DBő™įŽĺ∂Ľ≠‘≤£¨°—D”Žx÷ŠŌŗĹĽ”ŕĶ„M£¨N£®Ķ„M‘ŕĶ„NĶń◊ů≤ŗ£©£¨Ń¨Ĺ”CN£¨ĶĪMN=CN Ī£¨«ů»ŮĹ«°ŌMNCĶń∂» ż£Ľ
£®3£©»ÁÕľ3£¨‘ŕ£®2£©ĶńŐűľĢŌ¬£¨∆Ĺ“∆÷ĪŌŖCNĺ≠ĻżĶ„A£¨”ŽŇ◊őÔŌŖŌŗĹĽ”ŕŃŪ“ĽĶ„E£¨ĻżĶ„A◊ųx÷ŠĶń∆Ĺ––ŌŖm£¨ĻżĶ„£®©Ā3£¨0£©◊ųy÷ŠĶń∆Ĺ––ŌŖn£¨÷ĪŌŖm”Ž÷ĪŌŖnŌŗĹĽ”ŕĶ„S£¨Ķ„R‘ŕ÷ĪŌŖn…Ō£¨Ķ„P‘ŕEAĶń—”≥§ŌŖ…Ō£¨Ń¨Ĺ”SP£¨“‘SPő™ĪŖŌÚ…Ō◊ųĶ»ĪŖ°ųSPQ£¨Ń¨Ĺ”RQ£¨PR£¨»Ű°ŌQRS=60°„£¨ŌŖ∂őPRĶń÷–Ķ„K«°ļ√¬š‘ŕŇ◊őÔŌŖ…Ō£¨«ůQĶ„◊ÝĪÍ£ģ
°ĺīūįł°Ņ
£®1£©
Ĺ‚£ļ…ŤĻż◊ÝĪÍ‘≠Ķ„O£¨Ķ„A£®6£¨©Ā6 ![]() £©£¨«““‘y÷Šő™∂‘≥∆÷ŠĶńŇ◊őÔŌŖő™y=ax2£¨
£©£¨«““‘y÷Šő™∂‘≥∆÷ŠĶńŇ◊őÔŌŖő™y=ax2£¨
‘Ú©Ā6 ![]() =36a£¨
=36a£¨
°ŗa=©Ā ![]() £¨
£¨
°ŗy=©Ā ![]() x2
x2
£®2£©
Ĺ‚£ļ»ÁÕľ2÷–£¨◊ųCF°ÕMN”ŕF£¨…Ť°—D”Žx÷ŠĶńĹĽĶ„ő™£®x£¨0£©£¨D£®m£¨©Ā ![]() m2£©£ģ
m2£©£ģ
‘Ú”–£®x©Ām£©2+£® ![]() m2£©2=m2+£®©Ā
m2£©2=m2+£®©Ā ![]() m2+
m2+ ![]() £©2£¨
£©2£¨
’ŻņŪĶ√x2©Ā2mx+m2©Ā3=0£¨
°ŗx=m+ ![]() ĽÚm©Ā
ĽÚm©Ā ![]() £¨
£¨
°ŗN£®m+ ![]() £¨0£©£¨M£®m©Ā
£¨0£©£¨M£®m©Ā ![]() £¨0£©
£¨0£©
°ŗMN=2 ![]() £¨
£¨
‘ŕRt°ųCFN÷–£¨°Ŗ°ŌCFN=90°„£¨CN=MN=2 ![]() £¨CF=
£¨CF= ![]() £¨
£¨
°ŗCN=2CF£¨
°ŗ°ŌCNF=30°„
£®3£©
Ĺ‚£ļ»ÁÕľ3÷–£¨
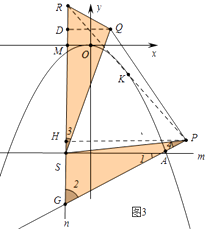
”…Ő‚“‚Ņ…÷™∆Ĺ“∆÷ĪŌŖCNĺ≠ĻżĶ„AĶń÷ĪŌŖĶńĹ‚őŲ Ĺő™y= ![]() x©Ā8
x©Ā8 ![]() £¨
£¨
ľ«÷ĪŌŖy= ![]() x©Ā8
x©Ā8 ![]() ”Ž÷ĪŌŖx=©Ā3ĶńĹĽĶ„ő™G£¨‘ÚG£®©Ā3£¨©Ā9
”Ž÷ĪŌŖx=©Ā3ĶńĹĽĶ„ő™G£¨‘ÚG£®©Ā3£¨©Ā9 ![]() £©£¨
£©£¨
°Ŗm°őx÷Š£¨«“ĻżĶ„A£®6£¨©Ā6 ![]() £©£¨
£©£¨
°ŗS£®©Ā3£¨©Ā6 ![]() £©£¨
£©£¨
°ŗSG=3 ![]() £¨AS=9£¨
£¨AS=9£¨
°ŗtan°Ō2= ![]() =
= ![]() £¨
£¨
°ŗ°Ō2=60°„£¨
°ŗ°Ō1=30°„£¨
°Ŗ°ŌQRS=60°„
°ŗ°ŌQRS=°Ō2£¨
°Ŗ°ŌRSQ+°ŌQSP=°Ō2+°ŌSPG£¨°ŌQSP=°Ō2=60°„£¨
°ŗ°Ō3=°Ō4£¨
‘ŕ°ųSQRļÕ°ųPSG÷–£¨
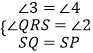 £¨
£¨
°ŗ°ųSQR°’°ųPSH
°ŗSR=PG£¨RQ=SG£¨
°ŗRQ=SG=3 ![]() £¨◊ųDQ°Õn”ŕD£¨
£¨◊ųDQ°Õn”ŕD£¨
°ŗQRD=60°„£¨
°ŗDQ= ![]() DR=
DR= ![]() RQ=
RQ= ![]() £¨
£¨
°ŗRD= ![]() QR=
QR= ![]() £¨
£¨
°Ŗn «Ļż£®©Ā3£¨0£©”Žy÷Š∆Ĺ––Ķń÷ĪŌŖ£¨…ŤR£®©Ā3£¨b£©£¨ľ«n”Žx÷ŠĶńĹĽĶ„ő™M£¨‘ÚRM=b£¨
°ŖS£®©Ā3£¨©Ā6 ![]() £©£¨
£©£¨
°ŗMS=6 ![]() £¨
£¨
°ŗSR=RM+MS=b+6 ![]() =PG£¨◊ųPH°Õn”ŕH£¨
=PG£¨◊ųPH°Õn”ŕH£¨
°Ŗ°Ō2=60°„£¨
°ŗGH= ![]() PG=
PG= ![]() £®b+6
£®b+6 ![]() £©£¨
£©£¨
°ŗMH=MG©ĀHG=9 ![]() ©Ā
©Ā ![]() £®b+6
£®b+6 ![]() £©=6
£©=6 ![]() ©Ā
©Ā ![]() b£¨
b£¨
°ŗP£®6+ ![]() b£¨
b£¨ ![]() b©Ā6
b©Ā6 ![]() £©£¨
£©£¨
°ŖK «PR÷–Ķ„£¨
°ŗK£® ![]() +
+ ![]() b£¨
b£¨ ![]() b©Ā3
b©Ā3 ![]() £©£¨
£©£¨
ő™Ńň∑ĹĪ„£¨ľ«K£®x£¨y£©£¨ľīx= ![]() +
+ ![]() b£¨y=
b£¨y= ![]() b©Ā3
b©Ā3 ![]() £¨ŌŻ»•bĶ√y=
£¨ŌŻ»•bĶ√y= ![]() x©Ā
x©Ā ![]()
![]() £¨
£¨
°ŗ÷–Ķ„K‘ŕ÷ĪŌŖy= ![]() ©Ā
©Ā ![]() …Ō‘ň∂Į£¨
…Ō‘ň∂Į£¨
”… 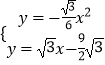 ŌŻ»•yĶ√ĶĹx2+6x©Ā27=0£¨
ŌŻ»•yĶ√ĶĹx2+6x©Ā27=0£¨
°ŗx=3ĽÚ©Ā9£®…Š∆ķ£©£¨
°ŗx=3£¨īķ»Žx= ![]() +
+ ![]() bĶ√ĶĹb=2
bĶ√ĶĹb=2 ![]() £¨
£¨
°ŗRM=2 ![]() £¨DM=RM©ĀRD=2
£¨DM=RM©ĀRD=2 ![]() ©Ā
©Ā ![]()
![]() =
= ![]()
![]() £¨
£¨
°Ŗ ![]() ©Ā3=
©Ā3= ![]() £¨
£¨
°ŗĶ„QĶń◊ÝĪÍő™£® ![]() £¨
£¨ ![]()
![]() £©
£©
°ĺĹ‚őŲ°Ņ£®1£©…ŤĻż◊ÝĪÍ‘≠Ķ„O£¨Ķ„A£®6£¨©Ā6 ![]() £©£¨«““‘y÷Šő™∂‘≥∆÷ŠĶńŇ◊őÔŌŖő™y=ax2 £¨ Ķ„Aīķ»Ž«ů≥ŲaľīŅ…£ģ£®2£©»ÁÕľ2÷–£¨◊ųCF°ÕMN”ŕF£¨…Ť°—D”Žx÷ŠĶńĹĽĶ„ő™£®x£¨0£©£¨D£®m£¨©Ā
£©£¨«““‘y÷Šő™∂‘≥∆÷ŠĶńŇ◊őÔŌŖő™y=ax2 £¨ Ķ„Aīķ»Ž«ů≥ŲaľīŅ…£ģ£®2£©»ÁÕľ2÷–£¨◊ųCF°ÕMN”ŕF£¨…Ť°—D”Žx÷ŠĶńĹĽĶ„ő™£®x£¨0£©£¨D£®m£¨©Ā ![]() m2£©£¨łýĺ›įŽĺ∂ŌŗĶ»Ń–≥Ų∑Ĺ≥Ő£¨«ů≥ŲM°ĘN◊ÝĪÍ£¨Õ∆≥ŲMN=2
m2£©£¨łýĺ›įŽĺ∂ŌŗĶ»Ń–≥Ų∑Ĺ≥Ő£¨«ů≥ŲM°ĘN◊ÝĪÍ£¨Õ∆≥ŲMN=2 ![]() £¨‘ŕRt°ųCFN÷–£¨”…CN=2CFÕ∆≥Ų°ŌFNC=30°„ľīŅ…Ĺ‚ĺŲő Ő‚£ģ£®3£©»ÁÕľ3÷–£¨”…Ő‚“‚Ņ…÷™∆Ĺ“∆÷ĪŌŖCNĺ≠ĻżĶ„AĶń÷ĪŌŖĶńĹ‚őŲ Ĺő™y=
£¨‘ŕRt°ųCFN÷–£¨”…CN=2CFÕ∆≥Ų°ŌFNC=30°„ľīŅ…Ĺ‚ĺŲő Ő‚£ģ£®3£©»ÁÕľ3÷–£¨”…Ő‚“‚Ņ…÷™∆Ĺ“∆÷ĪŌŖCNĺ≠ĻżĶ„AĶń÷ĪŌŖĶńĹ‚őŲ Ĺő™y= ![]() x©Ā8
x©Ā8 ![]() £¨ľ«÷ĪŌŖy=
£¨ľ«÷ĪŌŖy= ![]() x©Ā8
x©Ā8 ![]() ”Ž÷ĪŌŖx=©Ā3ĶńĹĽĶ„ő™G£¨‘ÚG£®©Ā3£¨©Ā9
”Ž÷ĪŌŖx=©Ā3ĶńĹĽĶ„ő™G£¨‘ÚG£®©Ā3£¨©Ā9 ![]() £©£¨”…°ųSQR°’°ųPSH£¨Õ∆≥ŲSR=PG£¨RQ=SG£¨Õ∆≥ŲRQ=SG=3
£©£¨”…°ųSQR°’°ųPSH£¨Õ∆≥ŲSR=PG£¨RQ=SG£¨Õ∆≥ŲRQ=SG=3 ![]() £¨◊ųDQ°Õn”ŕD£¨ľ«n”Žx÷ŠĶńĹĽĶ„ő™M£¨‘ÚRM=b£¨”…S£®©Ā3£¨©Ā6
£¨◊ųDQ°Õn”ŕD£¨ľ«n”Žx÷ŠĶńĹĽĶ„ő™M£¨‘ÚRM=b£¨”…S£®©Ā3£¨©Ā6 ![]() £©£¨Õ∆≥ŲMS=6
£©£¨Õ∆≥ŲMS=6 ![]() £¨Ņ…Ķ√P£®6+
£¨Ņ…Ķ√P£®6+ ![]() b£¨
b£¨ ![]() b©Ā6
b©Ā6 ![]() £©£¨‘Ŕ«ů≥ŲPR÷–Ķ„k◊ÝĪÍ£¨÷§√ųk‘ŕ÷ĪŌŖy=
£©£¨‘Ŕ«ů≥ŲPR÷–Ķ„k◊ÝĪÍ£¨÷§√ųk‘ŕ÷ĪŌŖy= ![]() ©Ā
©Ā ![]() …Ō‘ň∂Į£¨”…
…Ō‘ň∂Į£¨”…  ŌŻ»•yĶ√ĶĹx2+6x©Ā27=0£¨x=3ĽÚ©Ā9£®…Š∆ķ£©£¨x=3£¨īķ»Žx=
ŌŻ»•yĶ√ĶĹx2+6x©Ā27=0£¨x=3ĽÚ©Ā9£®…Š∆ķ£©£¨x=3£¨īķ»Žx= ![]() +
+ ![]() bĶ√ĶĹb=2
bĶ√ĶĹb=2 ![]() £¨”…īňľīŅ…Ĺ‚ĺŲő Ő‚£ģ
£¨”…īňľīŅ…Ĺ‚ĺŲő Ő‚£ģ
°ĺŅľĶ„ĺęőŲ°ŅĻō”ŕĪĺŐ‚Ņľ≤ťĶń∂ĢīőļĮ żĶńÕľŌůļÕ∂ĢīőļĮ żĶń–‘÷ £¨–Ť“™ŃňĹ‚∂ĢīőļĮ żÕľŌŮĻōľŁĶ„£ļ1°ĘŅ™Ņŕ∑ĹŌÚ2°Ę∂‘≥∆÷Š 3°Ę∂•Ķ„ 4°Ę”Žx÷ŠĹĽĶ„ 5°Ę”Žy÷ŠĹĽĶ„£Ľ‘Ųľű–‘£ļĶĪa>0 Ī£¨∂‘≥∆÷Š◊ůĪŖ£¨yňśx‘Ųīů∂Ýľű–°£Ľ∂‘≥∆÷Š”“ĪŖ£¨yňśx‘Ųīů∂Ý‘Ųīů£ĽĶĪa<0 Ī£¨∂‘≥∆÷Š◊ůĪŖ£¨yňśx‘Ųīů∂Ý‘Ųīů£Ľ∂‘≥∆÷Š”“ĪŖ£¨yňśx‘Ųīů∂Ýľű–°≤Ňń‹Ķ√≥Ų’ż»∑īūįł£ģ



| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨Ķ»—Ł»żĹ«–őABC÷–£¨AC=BC=10£¨AB=12£ģ
£®1£©∂Į ÷≤Ŕ◊ų£ļņŻ”√≥ŖĻś◊ų“‘BCő™÷Īĺ∂Ķń°—O£¨°—OĹĽAB”ŕĶ„D£¨°—OĹĽAC”ŕĶ„E£¨≤Ę«“ĻżĶ„D◊ųDF°ÕACĹĽAC”ŕĶ„F£ģ
£®2£©«ů÷§£ļ÷ĪŌŖDF «°—OĶń«–ŌŖ£Ľ
£®3£©Ń¨Ĺ”DE£¨ľ«°ųADEĶń√śĽżő™S1 £¨ ňńĪŖ–őDECBĶń√śĽżő™S2 £¨ «ů ![]() Ķń÷Ķ£ģ
Ķń÷Ķ£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ–°«Ņ÷ņŃĹ√∂÷ Ķōĺý‘»ĶńųĽ◊”£¨√ŅłŲųĽ◊”ĶńŃýłŲ√ś…Ō∑÷ĪūŅŐ”–1ĶĹ6ĶńĶ„ ż£¨‘ÚŃĹ√∂ųĽ◊”Ķ„ żŌŗÕ¨ĶńłŇ¬ ő™
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨AB=4cm£¨AC=BD=3cm£ģ°ŌCAB=°ŌDBA=60°„£¨Ķ„P‘ŕŌŖ∂őAB…Ō“‘1cm/sĶńňŔ∂»”…Ķ„AŌÚĶ„B‘ň∂Į£¨Õ¨ Ī£¨Ķ„Q‘ŕŌŖ∂őBD…Ō”…Ķ„BŌÚĶ„D‘ň∂Į£ģňŁ√«‘ň∂ĮĶń Īľšő™t£®s£©£¨‘ÚĶ„QĶń‘ň∂ĮňŔ∂»ő™ cm/s£¨ ĻĶ√A°ĘC°ĘP»żĶ„ĻĻ≥…Ķń»żĹ«–ő”ŽB°ĘP°ĘQ»żĶ„ĻĻ≥…Ķń»żĹ«–ő»ęĶ»£ģ

≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ1£ļ‘ŕňńĪŖ–őABCD÷–£¨AB£ĹAD£¨°ŌBAD£Ĺ120°„£¨°ŌB£Ĺ°ŌADC£Ĺ90°„£ģE°ĘF∑÷Īū «BC°ĘCD…ŌĶńĶ„£ģ«“°ŌEAF£Ĺ60°„£ģŐĹĺŅÕľ÷–ŌŖ∂őBE°ĘEF°ĘFD÷ģľšĶń żŃŅĻōŌĶ£ģ
–°ÕűÕ¨—ßŐĹĺŅīňő Ő‚Ķń∑Ĺ∑® «£¨—”≥§FDĶĹĶ„G£¨ ĻDG£ĹBE£ģѨŊAG£¨Ō»÷§√ų°ųABE°’°ųADG£¨‘Ŕ÷§√ų°ųAEF°’°ųAGF£¨Ņ…Ķ√≥ŲĹŠ¬Ř£¨ňŻĶńĹŠ¬Ř”¶ «°° °°£Ľ

ŐĹňų—”…ž£ļ
»ÁÕľ2£¨»Ű‘ŕňńĪŖ–őABCD÷–£¨AB£ĹAD£¨°ŌB£ę°ŌD£Ĺ180°„£ģE°ĘF∑÷Īū «BC°ĘCD…ŌĶńĶ„£¨«“°ŌEAF£Ĺ![]() °ŌBAD£¨…Ō ŲĹŠ¬Ř «∑Ů»‘»Ľ≥…ŃĘ£¨≤ĘňĶ√ųņŪ”…£Ľ
°ŌBAD£¨…Ō ŲĹŠ¬Ř «∑Ů»‘»Ľ≥…ŃĘ£¨≤ĘňĶ√ųņŪ”…£Ľ
Ķľ ”¶”√£ļ
»ÁÕľ3£¨‘ŕń≥īőĺŁ ¬—›Ōį÷–£¨ĹĘÕßľ◊‘ŕ÷łĽ”÷––ń£®Oī¶£©ĪĪ∆ęőų30°„ĶńAī¶£¨ĹĘÕß““‘ŕ÷łĽ”÷––ńńŌ∆ę∂ę70°„ĶńBī¶£¨≤Ę«“ŃĹĹĘÕßĶĹ÷łĽ”÷––ńĶńĺŗņŽŌŗĶ»£¨Ĺ”ĶĹ––∂Į÷łŃÓļů£¨ĹĘÕßľ◊ŌÚ’ż∂ę∑ĹŌÚ“‘60ļ£ņÔ/–° ĪĶńňŔ∂»«įĹÝ£¨ĹĘÕß““—ōĪĪ∆ę∂ę50°„Ķń∑ĹŌÚ“‘80ļ£ņÔ/–° ĪĶńňŔ∂»«įĹÝ1.5–° Īļů£¨÷łĽ”÷––ńĻŘ≤‚ĶĹľ◊°Ę““ŃĹĹĘÕß∑÷ĪūĶĹīÔE£¨Fī¶£¨«“ŃĹĹĘÕß÷ģľšĶńľ–Ĺ«ő™70°„£¨ ‘«ůīň ĪŃĹĹĘÕß÷ģľšĶńĺŗņŽ£Ņ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ”–ŃĹŅť√śĽżŌŗÕ¨Ķń ‘—ťŐÔ£¨∑÷Īū ’ĽŮ Ŗ≤ň900kgļÕ1500kg£¨“—÷™Ķŕ“ĽŅť ‘—ťŐÔ√Ņń∂ ’ĽŮ Ŗ≤ňĪ»Ķŕ∂ĢŅť…Ŕ300kg£¨«ůĶŕ“ĽŅť ‘—ťŐÔ√Ņń∂ ’ĽŮ Ŗ≤ň∂ŗ…Ŕ«ßŅň£Ņ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņłýĺ›Ő‚“‚Ĺ‚īū
£®1£©»ÁÕľ1£¨‘ŕňńĪŖ–őABCD÷–£¨AB=AD£¨°ŌBAD=120°„£¨°ŌB=°ŌADC=90°„£¨E°ĘF∑÷Īū «BC°ĘCD…ŌĶńĶ„£¨«“°ŌEAF=60°„£¨—”≥§FDĶĹĶ„G£¨ ĻDG=BE£¨Ń¨Ĺ”AG£¨Ō»÷§√ų°ųABE°’°ųADG£¨‘Ŕ÷§√ų°ųAEF°’°ųAGF£¨Ņ…Ķ√ŌŖ∂őBE°ĘEF°ĘFD÷ģľšĶń żŃŅĻōŌĶő™ £ģ
£®2£©»ÁÕľ2£¨‘ŕňńĪŖ–őABCD÷–£¨AB=AD£¨°ŌB+°ŌD=180°„£¨E°ĘF∑÷Īū «BC°ĘCD…ŌĶńĶ„£¨«“°ŌEAF= ![]() °ŌBAD£¨ŌŖ∂őBE°ĘEF°ĘFD÷ģľšīś‘ŕ ≤√ī żŃŅĻōŌĶ£¨ő™ ≤√ī£Ņ
°ŌBAD£¨ŌŖ∂őBE°ĘEF°ĘFD÷ģľšīś‘ŕ ≤√ī żŃŅĻōŌĶ£¨ő™ ≤√ī£Ņ
£®3£©»ÁÕľ3£¨Ķ„A‘ŕĶ„OĶńĪĪ∆ęőų30°„ī¶£¨Ķ„B‘ŕĶ„OĶńńŌ∆ę∂ę70°„ī¶£¨«“AO=BO£¨Ķ„A—ō’ż∂ę∑ĹŌÚ“∆∂Į249√◊ĶĹīÔEī¶£¨Ķ„B—ōĪĪ∆ę∂ę50°„∑ĹŌÚ“∆∂Į334√◊ĶĹīÔĶ„Fī¶£¨ī”Ķ„OĻŘ≤‚ĶĹE°ĘF÷ģľšĶńľ–Ĺ«ő™70°„£¨łýĺ›£®2£©ĶńĹŠ¬Ř«ůE°ĘF÷ģľšĶńĺŗņŽ£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
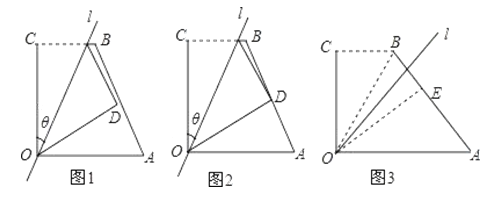
°ĺŐ‚ńŅ°Ņ£®‘ń∂Ń£©»ÁÕľ1£¨ňńĪŖ–őOABC÷–£¨OA=a£¨OC=3£¨BC=2£¨°ŌAOC=°ŌBCO=90°„£¨ĺ≠ĻżĶ„OĶń÷ĪŌŖlĹęňńĪŖ–ő∑÷≥…ŃĹ≤Ņ∑÷£¨÷ĪŌŖl”ŽOCňý≥…ĶńĹ«…Ťő™¶»£¨ĹęňńĪŖ–őOABCĶń÷ĪĹ«°ŌOCB—ō÷ĪŌŖl’ŘĶĢ£¨Ķ„C¬š‘ŕĶ„Dī¶£¨ő“√«į—’‚łŲ≤Ŕ◊ųĻż≥Őľ«ő™FZ [¶»£¨a ]
£®ņŪĹ‚£©»ŰĶ„D”ŽĶ„A÷ōļŌ£¨‘Ú’‚łŲ≤Ŕ◊ųĻż≥Őő™FZ [45°„£¨3]£Ľ
£®≥Ę ‘£©
£®1£©»ŰĶ„D«°ő™ABĶń÷–Ķ„£®»ÁÕľ2£©£¨«ů¶»£Ľ
£®2£©ĺ≠ĻżFZ[45°„£¨a]≤Ŕ◊ų£¨Ķ„B¬š‘ŕĶ„Eī¶£¨»ŰĶ„E‘ŕňńĪŖ–őOABCĶńĪŖAB…Ō£®»ÁÕľ3£©£¨«ů≥ŲaĶń÷Ķ£Ľ»ŰĶ„E¬š‘ŕňńĪŖ–őOABCĶńÕ‚≤Ņ£¨÷ĪĹ”–ī≥ŲaĶń»°÷Ķ∑∂őß.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™°ųABC‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ÷–ĶńőĽ÷√»ÁÕľňý ĺ£¨÷ĪŌŖlĻżĶ„M£®3£¨0£©«“∆Ĺ––”ŕy÷Š£ģ
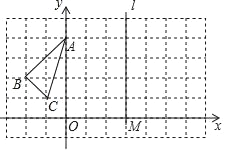
£®1£©◊ų≥Ų°ųABCĻō”ŕy÷Š∂‘≥∆Ķń°ųA1B1C1£¨≤Ę–ī≥Ų°ųA1B1C1łų∂•Ķ„Ķń◊ÝĪÍ£ģ
£®2£©»ÁĻŻĶ„PĶń◊ÝĪÍ «£®©Āa£¨0£©£¨∆š÷–a£ĺ0£¨Ķ„PĻō”ŕy÷ŠĶń∂‘≥∆Ķ„ «P1£¨Ķ„P1Ļō”ŕ÷ĪŌŖlĶń∂‘≥∆Ķ„ «P2£¨«ůP1P2Ķń≥§£ģ£®”√ļ¨aĶńīķ ż ĹĪŪ ĺ£©
£®3£©Õ®Ļżľ∆ň„ľ”“‘Ň–∂Ō£¨PP2Ķń≥§ĽŠ≤ĽĽŠňśĶ„PőĽ÷√ĶńĪšĽĮ∂ÝĪšĽĮ£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
įŔ∂»÷¬–Ň - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com