
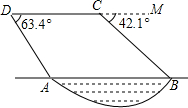
 如图,某勘测飞机为了测量一湖泊两端A、B的距离,飞机在距离湖面垂直高度为90米的点C处测得端点A的俯角为63.4°,然后沿着平行于AB的方向水平飞行了125米,在点D测得端点B的俯角为42.1°,求湖泊A、B两端的距离.
如图,某勘测飞机为了测量一湖泊两端A、B的距离,飞机在距离湖面垂直高度为90米的点C处测得端点A的俯角为63.4°,然后沿着平行于AB的方向水平飞行了125米,在点D测得端点B的俯角为42.1°,求湖泊A、B两端的距离.分析 过点C作CE⊥AB于点E,过点D作DF⊥AB于点F,利用三角函数求出AE的长,在Rt△BDF中,利用三角函数求出BF的长,进而可得AB的长.
解答  解:如图,过点C作CE⊥AB于点E,过点D作DF⊥AB于点F,
解:如图,过点C作CE⊥AB于点E,过点D作DF⊥AB于点F,
由题意可得∠ACD=63.4°,∠MDB=42.1°,CD=EF=125米,CE=DF=90米,
在Rt△AEC中,∠EAC=∠ACD=63.4°,
∵tan63.4°=$\frac{CE}{AE}$≈2.00,
∴AE=$\frac{CE}{tan63.4°}$≈$\frac{90}{2.00}$=45米,
在Rt△BDF中,∠FBD=∠MDB=42.1°,
∵tan42.1°=$\frac{DF}{BF}$≈0.90,
∴BF=$\frac{DF}{tan42.1°}$≈$\frac{90}{0.90}$=100米,
∴AB=EF-AE+BF=125-45+100=180米.
答:湖泊A、B两端的距离为180米.
点评 本题考查了解直角三角形的应用--仰角俯角问题,要求学生能借助仰角构造直角三角形并解直角三角形.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 32,31 | B. | 31,32 | C. | 31,31 | D. | 32,35 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我们知道平行四边形有很多性质,现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论.
我们知道平行四边形有很多性质,现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
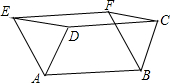 如图,已知?ABCD,以AD、BC为边,在它们的同侧作等边△ADE和等边△BCF,连接EF,求证:四边形ABFE和DCFE都是平行四边形.
如图,已知?ABCD,以AD、BC为边,在它们的同侧作等边△ADE和等边△BCF,连接EF,求证:四边形ABFE和DCFE都是平行四边形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com