
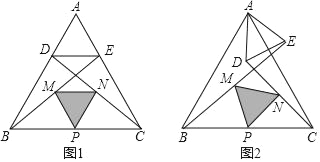
【题目】如图1,在等边△ABC中,点D,E分别在边AB,AC上,AD=AE,连接BE,CD,点M、N、P分别是BE、CD、BC的中点.
(1)观察猜想:图1中,△PMN的形状是 ;
(2)探究证明:把△ADE绕点A逆时针方向旋转到图2的位置,△PMN的形状是否发生改变?并说明理由;
(3)拓展延伸:把△ADE绕点A在平面内自由旋转,若AD=1,AB=3,请直接写出△PMN的周长的最大值.
【答案】(1) 等边三角形;(2) △PMN的形状不发生改变,仍然为等边三角形,理由见解析;(3)6
【解析】分析:(1)如图1,先根据等边三角形的性质得到AB=AC,∠ABC=∠ACB=60°,则BD=CE,再根据三角形中位线性质得PM∥CE,PM=![]() CE,PN∥AD,PN=
CE,PN∥AD,PN=![]() BD,从而得到PM=PN,∠MPN=60°,从而可判断△PMN为等边三角形;
BD,从而得到PM=PN,∠MPN=60°,从而可判断△PMN为等边三角形;
(2)连接CE、BD,如图2,先利用旋转的定义,把△ABD绕点A逆时针旋转60°可得到△CAE,则BD=CE,∠ABD=∠ACE,与(1)一样可得PM=PN,∠BPM=∠BCE,∠CPN=∠CBD,则计算出∠BPM+∠CPN=120°,从而得到∠MPN=60°,于是可判断△PMN为等边三角形.
(3)利用AB﹣AD≤BD≤AB+AD(当且仅当点B、A、D共线时取等号)得到BD的最大值为4,则PN的最大值为2,然后可确定△PMN的周长的最大值.
详解:(1)如图1.
∵△ABC为等边三角形,∴AB=AC,∠ABC=∠ACB=60°.
∵AD=AE,∴BD=CE.
∵点M、N、P分别是BE、CD、BC的中点,
∴PM∥CE,PM=![]() CE,PN∥AD,PN=
CE,PN∥AD,PN=![]() BD,
BD,
∴PM=PN,∠BPM=∠BCA=60°,∠CPN=∠CBA=60°,
∴∠MPN=60°,∴△PMN为等边三角形;
故答案为:等边三角形;
(2)△PMN的形状不发生改变,仍然为等边三角形.理由如下:
连接CE、BD,如图2.
∵AB=AC,AE=AD,∠BAC=∠DAE=60°,
∴把△ABD绕点A逆时针旋转60°可得到△CAE,
∴BD=CE,∠ABD=∠ACE,
与(1)一样可得PM∥CE,PM=![]() CE,PN∥AD,PN=
CE,PN∥AD,PN=![]() BD,
BD,
∴PM=PN,∠BPM=∠BCE,∠CPN=∠CBD,
∴∠BPM+∠CPN=∠CBD+∠CBD=∠ABC﹣∠ABD+∠ACB+∠ACE=60°+60°=120°,∴∠MPN=60°,∴△PMN为等边三角形.
(3)∵PN=![]() BD,∴当BD的值最大时,PN的值最大.
BD,∴当BD的值最大时,PN的值最大.
∵AB﹣AD≤BD≤AB+AD(当且仅当点B、A、D共线时取等号)
∴BD的最大值为1+3=4,∴PN的最大值为2,∴△PMN的周长的最大值为6.



科目:初中数学 来源: 题型:
【题目】我们知道,对于一个图形通过不同的方法计算图形的面积,可以得到一个数学等式,例如由图 1 可以得到 (a 2b)(a b) a![]() 3ab 2b
3ab 2b![]() ,请解答下列问题:
,请解答下列问题:

(1)写出图 2 所表示的数学等式: ;
(2)已知 a b c 12 ,ab bc ac 40 ,利用(1)中所得结论.求a![]() b
b![]() c
c![]() 的值;
的值;
(3)图 3 中给出了若干个边长为 a 和边长为 b 的小正方形纸片、若干个长为 b 宽为 a 的长方 形纸片,选用这些纸片拼出一个图形,使得它的面积是 2a ![]() 7ab 3b
7ab 3b ![]() .画出该图形,并利用该图形把多项式 2a
.画出该图形,并利用该图形把多项式 2a![]() 7ab 3b
7ab 3b![]() 分解因式.
分解因式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个寻宝游戏的寻宝通道如图①所示,通道由在同一平面内的AB,BC,CA,OA, OB,OC组成。为记录寻宝者的行进路线,在BC的中点M处放置了一台定位仪器,设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图像大致如图②所示,则寻宝者的行进路线可能为:

A. A→O→B B. B→A→C C. B→O→C D. C→B→O
查看答案和解析>>
科目:初中数学 来源: 题型:
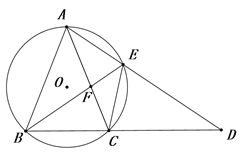
【题目】如图,△ABC内接于⊙O,且AB=AC.延长BC到点D,使CD=CA,连接AD交⊙O于点E.
(1)求证:△ABE≌△CDE;
(2)填空:
①当∠ABC的度数为 时,四边形AOCE是菱形;
②若AE=6,BE=8,则EF的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将四张边长各不相同的正方形纸片按如图方式放入矩形ABCD内(相邻纸片之间互不重叠也无缝隙),未被四张正方形纸片覆盖的部分用阴影表示,设右上角与左下角阴影部分的周长的差为l.若知道l的值,则不需要测量就能知道周长的正方形的标号为( )

A.①B.②C.③D.④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里=0.5千米,则该沙田的面积为________________平方千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知P为正方形ABCD外的一点,PA=1,PB=2,将△ABP绕点B顺时针旋转90°,使点P旋转至点P′,且AP′=3,则∠BP′C的度数为 ( )
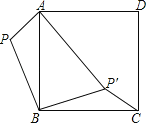
A.105° B.112.5° C.120° D.135°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com