
 如图,等边△ABC的边长为10,D为AC上任意一点,延长AB至点E,使BE=CD,连接DE交BC于点P.
如图,等边△ABC的边长为10,D为AC上任意一点,延长AB至点E,使BE=CD,连接DE交BC于点P.分析 (1)作DM∥AB交BC于M,可得出△CDM是等边三角形,BE=DM,再求出△DPM≌△EPB,由全等三角形的性质即可得出结论;
(2)根据△BPE≌△MPD得到PM=BP,再证明△CDM是等边三角形,进而得到答案.
解答 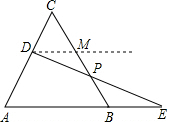 (1)证明:作DM∥AB交BC于M,
(1)证明:作DM∥AB交BC于M,
∵△ABC是等边三角形,
∴∠C=∠A=∠ABC=60°,
∵DM∥AB,
∴∠CDM=∠A=60°,
∴△CDM是等边三角形,
∴CD=DM,
∵BE=CD,
∴BE=DM,
∵DM∥AB,
∴∠E=∠MDP,∠EBP=∠DMP,
在△DPM与△EPB中,
∵$\left\{\begin{array}{l}{∠E=∠MDP}\\{BE=DM}\\{∠EBP=∠DMP}\end{array}\right.$,
∴△DPM≌△EPB(ASA),
∴DP=PE.
(2)解:由(1)得△BPE≌△MPD,
∴PM=BP,
∵∠C=∠CMD=60°,
∴∠CDM=60°,
∴△CDM是等边三角形,
∴CD=CM=DM,
∵D为AC的中点,
∴CD=CM=$\frac{1}{2}$AC=$\frac{1}{2}$BC=5,
∴BP=$\frac{1}{2}$BF=2.5.
点评 本题考查的是全等三角形的判定与性质以及等边三角形的性质,根据题意作出辅助线,构造出等边三角形是解答此题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
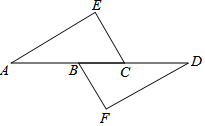 如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,AE=DF,∠A=∠D,AB=DC.求证:四边形BFCE是平行四边形.
如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,AE=DF,∠A=∠D,AB=DC.求证:四边形BFCE是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
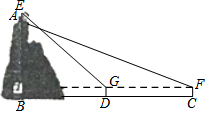 某综合实践活动小组实地测量了某山峰与中心广场的相对高度AB,其测量步骤如下:
某综合实践活动小组实地测量了某山峰与中心广场的相对高度AB,其测量步骤如下:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
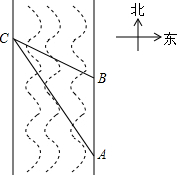 在2014年6月23日第十届保护韩江母亲河徒步节上,如图所示,某同学为了测得一段南北流向的河段的宽,在河东岸点A处观测到河对岸水边有一点C,测得C在A北偏西31°的方向上,沿河岸向北前行40米到达B处,测得C在B北偏西45°的方向上,请你根据以上数据,求这段河段的宽度.(参考数值:tan31°≈$\frac{3}{5}$)
在2014年6月23日第十届保护韩江母亲河徒步节上,如图所示,某同学为了测得一段南北流向的河段的宽,在河东岸点A处观测到河对岸水边有一点C,测得C在A北偏西31°的方向上,沿河岸向北前行40米到达B处,测得C在B北偏西45°的方向上,请你根据以上数据,求这段河段的宽度.(参考数值:tan31°≈$\frac{3}{5}$)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 先完成下列填空,再在同一直角坐标系中画出以下函数的图象(不必再列表)
先完成下列填空,再在同一直角坐标系中画出以下函数的图象(不必再列表)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com