
【题目】数学课上,李老师出示了如下框中的题目.
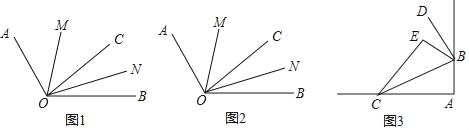
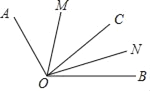
如图1,在∠AOB的内部有一条射线OC把∠AOB分成两个角,射线OM、ON分别平分∠AOC、∠BOC,试探究∠MON与∠AOB之间的数量关系,并说明理由.
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论:
①请你在下表中填上当∠AOB为60°、90°、120°时∠MON的大小:
∠AOB的度数 | 60° | 90° | 120° |
∠MON的度数 |
|
|
|
②探索发现:无论∠AOB的度数是多少,∠MON与∠AOB的数量关系是不变的,请你直接写出结论:
∠MON ∠AOB.
(2)特例启发,解答题目:
如图2,如果∠AOB=α,请你求∠MON的大小(用α表示).
(3)拓展结论,设计新题:
如图3,把一张报纸的一角斜折过去,使A点落在E点处,BC为折痕,BD是∠EBM的平分线,求∠CBD的度数.
【答案】(1)①30°,45°,60°;②![]() ;(2)∠MON=
;(2)∠MON=![]() α;(3)∠CBE+∠EBD=90°.
α;(3)∠CBE+∠EBD=90°.
【解析】
(1)①②根据角平分线的定义即可得到结论;
(2)由角平分线的定义即可得到结论;
(3)先根据折叠的性质得到∠CBA=∠CBE=![]() ∠ABE,再根据平分线的定义得到∠EBD=∠DBM=
∠ABE,再根据平分线的定义得到∠EBD=∠DBM=![]() ∠MBE,则∠CBE+∠EBD=
∠MBE,则∠CBE+∠EBD=![]() (∠ABE+∠MBE)=
(∠ABE+∠MBE)=![]() ∠ABM,然后根据平角定义进行计算.
∠ABM,然后根据平角定义进行计算.
(1)①∵∠MOC=![]() ∠AOC,∠NOC=
∠AOC,∠NOC=![]() ∠BOC,
∠BOC,
∴∠MON=∠MOC+∠NOC=![]() ∠AOC+
∠AOC+![]() ∠BOC=
∠BOC=![]() ∠AOB,
∠AOB,
当∠AOB=60°时,∠MON=![]() ×60°=30°,
×60°=30°,
当∠AOB=90°时,∠MON=![]() ×90°=45°,
×90°=45°,
当∠AOB=120°时,∠MON=![]() ×120°=60°;
×120°=60°;
②由①知,∠MON=![]() ∠AOB,
∠AOB,
(2)由(1)②知,∠MON=![]() ∠AOB,
∠AOB,
∴∠MON=![]() α;
α;
(3)∵A点落在E点处,BC为折痕,
∴∠CBA=∠CBE=![]() ∠ABE,
∠ABE,
∵D是∠EBM的平分线,
∴∠EBD=∠DBM=![]() ∠MBE,
∠MBE,
∴∠CBE+∠EBD=![]() (∠ABE+∠MBE)=
(∠ABE+∠MBE)=![]() ∠ABM=
∠ABM=![]() ×180°=90°.
×180°=90°.


 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:
【题目】点A,O,B依次在直线MN上,如图1,现将射线OA绕点O顺时针方向以每秒10°的速度旋转,同时射线OB绕着点O按逆时针方向以每秒15°的速度旋转,直线MN保持不动,如图2,设旋转时间为t秒(t≤12).
(1)在旋转过程中,当t=2时,求∠AOB的度数.
(2)在旋转过程中,当∠AOB=105°时,求t的值.
(3)在旋转过程中,当OA或OB是某一个角(小于180°)的角平分线时,求t的值.
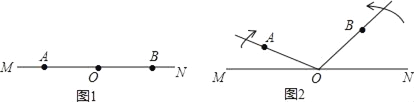
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:A是以BC为直径的圆上的一点,BE是⊙O的切线,CA的延长线与BE交于E点,F是BE的中点,延长AF,CB交于点P. 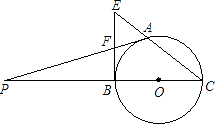
(1)求证:PA是⊙O的切线;
(2)若AF=3,BC=8,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ACB和△AED中,AC=BC,AE=DE,∠ACB=∠AED=90°,点E在AB上,F是线段BD的中点,连接CE、FE.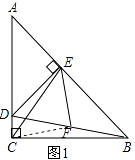
(1)若AD=3 ![]() ,BE=4,求EF的长;
,BE=4,求EF的长;
(2)求证:CE= ![]() EF;
EF;
(3)将图1中的△AED绕点A顺时针旋转,使AED的一边AE恰好与△ACB的边AC在同一条直线上(如图2),连接BD,取BD的中点F,问(2)中的结论是否仍然成立,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在求1+3+32+33+34+35+36+37+38的值时,张红发现:从第二个加数起每一个加数都是前一个加数的3倍,于是她假设:S=1+3+32+33+34+35+36+37+38 ①,然后在①式的两边都乘以3,得:3S=3+32+33+34+35+36+37+38+39 ②,
②一①得:3S―S=39-1,即2S=39-1,
∴S=![]() .
.
得出答案后,爱动脑筋的张红想:如果把“3”换成字母m(m≠0且m≠1),能否求出1+m+m2+m3+m4+…+m2016的值?如能求出,其正确答案是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
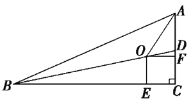
【题目】如图,在![]() ABC中,∠C=90,BD平分∠ABC,交AC于D,点O、E、F分别在BD、BC、
ABC中,∠C=90,BD平分∠ABC,交AC于D,点O、E、F分别在BD、BC、
AC上,且四边形OECF是正方形.
(1)求证:点O在∠BAC的平分线上;
(2)若AC=5,BC=12,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市美化工程招标时,有甲、乙两个工程队投标.经测算:甲队单独完成这项工程需要60天;若由甲队先做20天,剩下的工程由甲、乙合做24天可完成.
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天,需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱?还是由甲乙两队全程合作完成该工程省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有16个只有颜色不同的球,其中红球有x个,白球有2x个,其他均为黄球,现甲从布袋中随机摸出一个球,若是红球则甲同学获胜,甲同学把摸出的球放回并搅匀,由乙同学随机摸出一个球,若为黄球,则乙同学获胜。
(1)当X=3时,谁获胜的可能性大?
(2)当x为何值时,游戏对双方是公平的?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com