练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．如图，四边形ABCD中，AD∥BC，BA，CD的延长线相交于点E，若AD=2，BC=3，BA=2.5，则AE=5，理由是：相似三角形的性质．

    分析 根据相似三角形的判定和性质，即可得到结论．

    解答 解：∵AD∥BC，
    ∴△EAD∽△EBC，
    ∴$\frac{AE}{BE}=\frac{AD}{BC}$，
    即$\frac{AE}{AE+2.5}=\frac{2}{3}$，
    解得：AE=5，
    理由：相似三角形的性质，
    故答案为：5，相似三角形的性质．

    点评 本题考查了相似三角形的判定和性质，熟练掌握相似三角形的判定和性质是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    7．计算
    （1）-18+（-14）-（-28）-13；               （2）（-32）×（$\frac{3}{16}$-$\frac{5}{8}$+$\frac{7}{4}$）；
    （3）-$\frac{5}{2}$÷$\frac{28}{5}$÷（-2）×（-$\frac{5}{14}$）；                 （4）-14-（1-0.5）×$\frac{1}{3}$×[1-（-2）2]．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

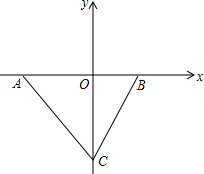    8．如图，在平面直角坐标系中，点D在y轴上，点C的坐标为（0，-4），直线AD平分∠BAC，线段OA、OB的长满足一元二次方程x2-5x+6=0的两根（OA＞OB）．
    （1）求OA、OB的长；
    （2）求直线AD的解析式；
    （3）坐标系上是否存在点P，使以P、D、A、C为顶点的平行四边形？若存在，请直接写出满足条件的点P；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图，在直角坐标系中，矩形ABCD的边AB与x轴重合，A（-3，0），C（3，2$\sqrt{3}$），P（6，0）是x轴正半轴上的一点，一动点E从原点O出发，以每秒1个单位长度的速度沿OA方向匀速运动，到达A点后，立即以原速度AO返回；另一动点F从P点出发，以每秒1个单位长度的速度沿PA方向匀运动，点E、F同时出发，当两点相遇时整个运动过程停止，在点E、F的运动过程中，以EF为边作等边△EFG，使△EFG和矩形ABCD在x轴的同侧，设运动的时间为t秒（t≥0）．
    （1）当t=1时，EF=6，当t=4时，EF=4；
    （2）当等边△EFG的边FG恰好经过点C时，求出此时的t值；
    （3）在运动过程，设等边△EFG和矩形ABCD重叠部分的面积为S，请求出当0≤t≤3时，S与t之间的函数关系式；
    （4）在整个过程中，当S满足2$\sqrt{3}$≤S≤7$\sqrt{3}$时，直接写出t的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．如图所示，已知正方形ABCD和正△AEF都内接于圆，EF与BC和CD分别交于G、H，则GH：EF=$\sqrt{3}$：3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．如图，求阴影部分的面积，它可以验证哪个公式？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．如图，已知等腰直角△ABC的直角边长与正方形MNPQ的边长均为10cm，AC与MN在同一直线上，开始时点A与点M重合，让△ABC沿着MN方向以每秒1cm的速度移动，最后点A与点N重合．
    （1）直接写出重叠部分周长y（cm）与运动时间x（秒）之间的函数关系式及自变量x的取值范围；
    （2）当运动时间为多少秒时，重叠部分周长等于△ABC周长的一半．（结果精确到1秒）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．一个立方体被一个平面截去一个三棱锥后，剩余几何体的顶点个数为7个、或8个、或9个、或10个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图是长春节某花园的平面图，花园长为100米，宽为50米，在它的四角各建有一个同样大小的正方形观光休息亭，四周建有与观光休息亭等宽的观光大道，其余部分（图中阴影部分）种植的是不同花草．若设观光休息亭的边长为a米，求种植花草部分的面积．

    查看答案和解析>>

    同步练习册答案