
如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根.
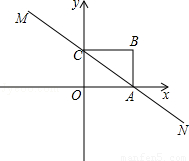
(1)求C点坐标;
(2)求直线MN的解析式;
(3)在直线MN上存在点P,使以点P,B,C三点为顶点的三角形是等腰三角形,请直接写出P点的坐标.
(1)C(0,6);(2)y=- x+6;(3)P1(4,3),P2(-
x+6;(3)P1(4,3),P2(- ,
, ),P3(
),P3( ,
, ),P4(
),P4( ,-
,- ).
).
【解析】
试题分析:
(1)通过解方程x2﹣14x+48=0可以求得OC=6,OA=8.则C(0,6);
(2)设直线MN的解析式是y=kx+b(k≠0).把点A、C的坐标分别代入解析式,列出关于系数k、b的方程组,通过解方程组即可求得它们的值;
(3)需要分类讨论:PB为腰,PB为底两种情况下的点P的坐标.根据等腰三角形的性质、两点间的距离公式以及一次函数图象上点的坐标特征进行解答.
试题解析:
(1)解方程x2-14x+48=0得
x1=6,x2=8
∵OA,OC(OA>OC)的长分别是一元二次方程x2-14x+48=0的两个实数根
∴OC=6,OA=8
∴C(0,6)
(2)设直线MN的解析式是y=kx+b(k≠0)
由(1)知,OA=8,则A(8,0)
∵点A、C都在直线MN上
∴
解得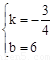 ,
,
∴直线MN的解析式为y=- x+6
x+6
(3)

∵A(8,0),C(0,6)
∴根据题意知B(8,6)
∵点P在直线MN y=- x+6上
x+6上
∴设P(a,-- a+6)
a+6)
当以点P,B,C三点为顶点的三角形是等腰三角形时,需要分类讨论:
①当PC=PB时,点P是线段BC的中垂线与直线MN的交点,则P1(4,3);
②当PC=BC时,a2+(- a+6-6)2=64
a+6-6)2=64
解得,a=± ,则P2(-
,则P2(- ,
, ),P3(
),P3( ,
, )
)
③当PB=BC时,(a-8)2+(- a+6-6)2=64
a+6-6)2=64
解得,a= ,则-
,则- a+6=-
a+6=-
∴P4( ,
, )
)
综上所述,符合条件的点P有:P1(4,3),P2(- ,
, ),P3(
),P3( ,
, ),P4(
),P4( ,-
,- )
)
考点:一次函数综合题.


科目:初中数学 来源: 题型:
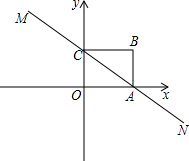 (2013•绥化)如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2-14x+48=0的两个实数根.
(2013•绥化)如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2-14x+48=0的两个实数根.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2-14x+48=0的两个实数根.
如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2-14x+48=0的两个实数根.查看答案和解析>>
科目:初中数学 来源: 题型:
如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根.
(1)求C点坐标;
(2)求直线MN的解析式;
(3)在直线MN上存在点P,使以点P,B,C三点为顶点的三角形是等腰三角形,请直接写出P点的坐标.

查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(黑龙江绥化卷)数学(解析版) 题型:解答题
如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根.

(1)求C点坐标;
(2)求直线MN的解析式;
(3)在直线MN上存在点P,使以点P,B,C三点为顶点的三角形是等腰三角形,请直接写出P点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com