
(12分)已知O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
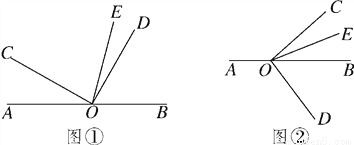
(1)如图①,若∠AOC=30°,求∠DOE的度数;
(2)在图①中,若∠AOC=a,直接写出∠DOE的度数(用含a的代数式表示);
(3)将图①中的∠DOC绕顶点O顺时针旋转至图②的位置.
①探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由;
②在∠AOC的内部有一条射线OF,且∠AOC-4∠AOF=2∠BOE+∠AOF,试确定∠AOF与∠DOE的度数之间的关系,说明理由.
科目:初中数学 来源:2017-2018学年甘肃省武威市凉州区洪祥镇九年级(上)期末数学试卷 题型:单选题
下列图形中,既是中心对称图形又是轴对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:人教版九年级下册 期中测试卷 题型:单选题
如图是一次函数y1=kx-b和反比例函数y2= 的图象,观察图象写出y1>y2时,x的取值范围是( )
的图象,观察图象写出y1>y2时,x的取值范围是( )

A. x>3 B. x>-2或x>3
C. x<-2或0<x<3 D. -2<x<0或x>3
D 【解析】由图可知,当一次函数的图象在反比例函数图象上方时对应的自变量的取值范围是: 或. 故选D.查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学北师大版上册:第3章 整式及其加减 单元测试卷 题型:填空题
当a=1,b=-2时,代数式2a+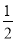 b2的值是________.
b2的值是________.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学北师大版上册:第3章 整式及其加减 单元测试卷 题型:单选题
填在下面各正方形中的四个数之间都有相同的规律,根据这种规律,m的值应是( )

A. 110 B. 158 C. 168 D. 178
B 【解析】试题解析: 根据排列规律,10下面的数是12,10右面的数是14, ∵8=2×4?0,22=4×6?2,44=6×8?4, ∴m=12×14?10=158. 故选B.查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学人教版上册:第4章 几何图形初步 单元测试卷 题型:解答题
观察下面由7个小正方体组成的图形,请你画出从正面、上面、左面看到的平面图形.

查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学人教版上册:第4章 几何图形初步 单元测试卷 题型:填空题
如图所示的图形中,柱体为_____(请填写你认为正确物体的序号).

查看答案和解析>>
科目:初中数学 来源:2017-2018学年山东省德州市六校七年级(上)第一次联考数学试卷 题型:解答题
先化简,再求值:  (4a2﹣2a﹣8)﹣(
(4a2﹣2a﹣8)﹣( a﹣1),其中a=1.
a﹣1),其中a=1.
查看答案和解析>>
科目:初中数学 来源:云南省楚雄州2017-2018学年上学期期末教学质量监测九年级数学试卷 题型:填空题
正方形网格中,∠AOB如图放置,则tan∠AOB=______________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com