
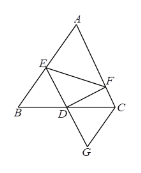
【题目】如图,在△ABC中,D为BC的中点,E为AB上一点,DF⊥DE交AC于点F,延长ED至点G,使GD=ED,连接CG.
(1)求证:BE=CG;
(2)求证:BE+CF>EF.
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
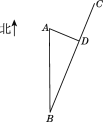
【题目】如图,某沿海城市A接到台风警报,在该城市正南方向260 km的B处有一台风中心,沿BC方向以15 km/h的速度向C移动,已知城市A到BC的距离AD=100 km,那么台风中心经过多长时间从B点移动到D点?如果在距台风中心30 km的圆形区域内都将受到台风的影响,正在D点休息的游人在接到台风警报后的几小时内撤离才可以免受台风的影响?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠1=∠2,EG 平分∠AEC.
(1)如图1,∠MAE=50°,∠FEG=15°,∠NCE=80°.试判断 EF 与 CD 的位置关系,并说明理由.
(2)如图2,∠MAE=135°,∠FEG=30°,当 AB∥CD 时,求∠NCE 的度数;
(3)如图2,试写出∠MAE、∠FEG、∠NCE 之间满足什么关系时,AB∥CD.
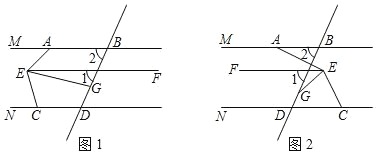
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平安路与幸福路是两条平行的道路,且都与新兴大街垂直,老街与小米胡同垂直,书店位于老街与小米胡同的交口处.如果小强同学站在平安路与新兴大街交叉路口,准备去书店,按图中的街道行走,最近的路程为( )

A. 300m B. 400m C. 500m D. 700m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学问题中,我们常用几何方法解决代数问题,借助数形结合的方法使复杂问题简单化.
材料一:我们知道|a|的几何意义是:数轴上表示数a的点到原点的距离;|a﹣b|的几何意义是:数轴上表示数a,b的两点之间的距离;|a+b|的几何意义是:数轴上表示数a,﹣b的两点之间的距离;根据绝对值的几何意义,我们可以求出以下方程的解.
(1)|x﹣3|=4
解:由绝对值的几何意义知:
在数轴上x表示的点到3的距离等于4
∴x1=3+4=7,x2=3﹣4=﹣1
(2)|x+2|=5
解:∵|x+2|=|x﹣(﹣2)|,∴其绝对值的几何意义为:在数轴上x表示的点到﹣2的距离等于5.∴x1=﹣2+5=3,x2=﹣2﹣5=﹣7
材料二:如何求|x﹣1|+|x+2|的最小值.
由|x﹣1|+|x+2|的几何意义是数轴上表示数x的点到表示数1和﹣2两点的距离的和,要使和最小,则表示数x的这点必在﹣2和1之间(包括这两个端点)取值.
∴|x﹣1|+|x+2|的最小值是3;由此可求解方程|x﹣1|+|x+2|=4,把数轴上表示x的点记为点P,由绝对值的几何意义知:当﹣2≤x≤1时,|x﹣1|+|x+2|恒有最小值3,所以要使|x﹣1|+|x+2|=4成立,则点P必在﹣2的左边或1的右边,且到表示数﹣2或1的点的距离均为0.5个单位.
故方程|x﹣1|+|x+2|=4的解为:x1=﹣2﹣0.5=﹣2.5,x2=1+0.5=1.5.
阅读以上材料,解决以下问题:
(1)填空:|x﹣3|+|x+2|的最小值为 ;
(2)已知有理数x满足:|x+3|+|x﹣10|=15,有理数y使得|y﹣3|+|y+2|+|y﹣5|的值最小,求x﹣y的值.
(3)试找到符合条件的x,使|x﹣1|+|x﹣2|+…+|x﹣n|的值最小,并求出此时的最小值及x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
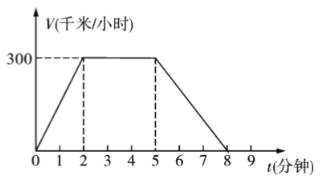
【题目】如图,是一辆列车在某次运行中速度![]() (千米/小时)关于时间
(千米/小时)关于时间![]() (分钟)的图象,根据图象回答下列问题.
(分钟)的图象,根据图象回答下列问题.
(1)列车共运行了多少分钟?
(2)列车开动后,匀速行驶了几分钟?第3分钟时的速度是多少?
(3)列车的速度从0千米/小时加速到300千米/小时,共用了多长时间?
(4)列车从第几分钟开始减速?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提升学生的艺术素养,学校计划开设四门艺术选修课:A.书法;B.绘画;C.乐器;D.舞蹈.为了解学生对四门功课的喜欢情况,在全校范围内随机抽取若干名学生进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).将数据进行整理,并绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:
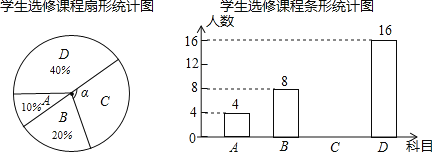
(1)本次调查的学生共有多少人?扇形统计图中∠α的度数是多少?
(2)请把条形统计图补充完整;
(3)学校为举办2018年度校园文化艺术节,决定从A.书法;B.绘画;C.乐器;D.舞蹈四项艺术形式中选择其中两项组成一个新的节目形式,请用列表法或树状图求出选中书法与乐器组合在一起的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com