
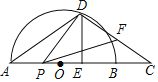
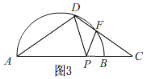
【题目】如图,AB是半圆O的直径,C是AB延长线上的点,AC的垂直平分线交半圆于点D,交AC于点E,连接DA,DC.已知半圆O的半径为3,BC=2.
(1)求AD的长.
(2)点P是线段AC上一动点,连接DP,作∠DPF=∠DAC,PF交线段CD于点F.当△DPF为等腰三角形时,求AP的长.
【答案】(1)AD=2![]() ;(2)当△DPF是等腰三角形时,AP的长为0或5或8﹣2
;(2)当△DPF是等腰三角形时,AP的长为0或5或8﹣2![]() .
.
【解析】
(1)先求出AC,进而求出AE=4,再用勾股定理求出DE即可得出结论;
(2)分三种情况,利用相似三角形得出比例式,即可得出结论
(1)如图1,连接OD,
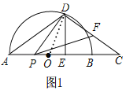
∵OA=OD=3,BC=2,
∴AC=8,
∵DE是AC的垂直平分线,
∴AE=![]() AC=4,
AC=4,
∴OE=AE﹣OA=1,
在Rt△ODE中,DE=![]() =2
=2![]() ;
;
在Rt△ADE中,AD=![]() =2
=2![]() ;
;
(2)当DP=DF时,如图2,
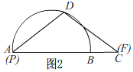
点P与A重合,F与C重合,则AP=0;
当DP=PF时,如图4,
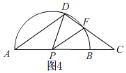
∴∠CDP=∠PFD,
∵DE是AC的垂直平分线,∠DPF=∠DAC,
∴∠DPF=∠C,
∵∠PDF=∠CDP,
∴△PDF∽△CDP,
∴∠DFP=∠DPC,
∴∠CDP=∠CPD,
∴CP=CD,
∴AP=AC﹣CP=AC﹣CD=AC﹣AD=8﹣2![]() ;
;
当PF=DF时,如图3,
∴∠FDP=∠FPD,
∵∠DPF=∠DAC=∠C,
∴△DAC∽△PDC,
∴![]() ,
,
∴![]() ,
,
∴AP=5,
即:当△DPF是等腰三角形时,AP的长为0或5或8﹣2![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,点 O 是△ABC 的边 AB 上一点,以 OB 为半径的⊙O 交 BC 于点 D,过点 D 的切线交 AC 于点 E,且 DE⊥AC.
(1)证明:AB=AC;
(2)设 AB=![]() cm,BC=2cm,当点 O 在 AB 上移动到使⊙O 与边 AC 所在直线相切时, 求⊙O 的半径.
cm,BC=2cm,当点 O 在 AB 上移动到使⊙O 与边 AC 所在直线相切时, 求⊙O 的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+2x+m﹣2=0有两个实数根,m为正整数,且该方程的根都是整数,则符合条件的所有正整数m的和为( )
A. 6 B. 5 C. 4 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
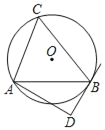
【题目】如图,⊙O的半径为5,△ABC是⊙O的内接三角形,AB=8.AD和过点B的切线互相垂直,垂足为D.
(1)求证:∠BAD+∠C=90°;
(2)求线段AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
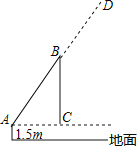
【题目】如图,吊车在水平地面上吊起货物时,吊绳BC与地面保持垂直,吊臂AB与水平线的夹角为64°,吊臂底部A距地面1.5m.(计算结果精确到0.1m,参考数据sin64°≈0.90,cos64°≈0.44,tan64°≈2.05)
(1)当吊臂底部A与货物的水平距离AC为5m时,吊臂AB的长为多少m.
(2)如果该吊车吊臂的最大长度AD为20m,那么从地面上吊起货物的最大高度是多少?(吊钩的长度与货物的高度忽略不计)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明同学用自制的直角三角形纸板DEF测量树AB的高度,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=8m,求树AB的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
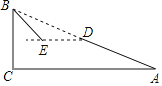
【题目】如图,斜坡AB长130米,坡度i=1:2.4,BC⊥AC,
(1)BC= m,AC= m;
(2)现在计划在斜坡AB的中点D处挖去部分坡体修建一个平行于水平线CA的平台DE和一条新的斜坡BE,若斜坡BE的坡角为30°,求平台DE的长;(精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.45)
≈2.45)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com