练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．如果把分式$\frac{{3n}^{2}}{m-n}$中的m和n都扩大3倍，那么分式的值（　　）
    A．不变B．扩大3倍C．缩小3倍D．扩大9倍

    分析 根据分式的性质，可得答案．

    解答 解：把分式$\frac{{3n}^{2}}{m-n}$中的m和n都扩大3倍，得
    $\frac{3（3n）^{2}}{3m-3n}$=$\frac{3×3n}{m-n}$，
    故选：B．

    点评 本题考查了分式的基本性质，把m，n分别换成3m，3n是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

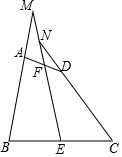    15．如图，在四边形ABCD中，AB=CD，E、F分别是BC、AD的中点，连结EF并延长，分别与BA，CD的延长线交于点M、N，证明：∠BME=∠CNE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．化简：$\frac{a+1}{{a}^{2}+1}$+$\frac{{（a+1）}^{3}}{{a}^{4}-1}$-$\frac{a-3}{a+1}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．圆锥的主视图如图所示（单位：cm），则这个圆锥的侧面积是（　　）
    A．15cm2B．15πcm2C．30πcm2D．60cm2

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．如图，将边长为4cm的正方形ABCD沿其对角线AC剪开，再把△ABC沿AD方向平移，得到△A′B′C′，若两个三角形重叠部分的面积是4cm2，则它移动的距离AA′等于（　　）
    A．3cmB．2.5cmC．1.5cmD．2cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

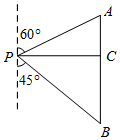    10．如图，小明同学在点P处测得教学楼A位于北偏东60°方向，办公楼B位于南偏东45°方向．小明沿正东方向前进60米到达C处，此时测得教学楼A恰好位于正北方向．办公楼B正好位于正南方向．求教学楼A与办公楼B之间的距离（60+20$\sqrt{3}$）米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

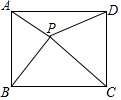    17．如图，点P是矩形ABCD内一点，连接PA、PB、PC、PD，已知AB=3，BC=4，设△PAB、△PBC、△PDA的面积分别为S1、S2、S3、S4，以下判断：
    ①PA+PB+PC+PD的最小值为10；
    ②若△PAB≌△PDC，则△PAD≌△PBC；
    ③若S1=S2，则S3=S4；
    ④若△PAB∽△PDA，则PA=2.4
    其中正确的是①②③④．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．反比例函数y=$\frac{k}{x}$的图象经过（-6，2）和（a，3），则a=-4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．计算：$\sqrt{12}$-2tan60°+（$\sqrt{2017}$-1）0-（$\frac{1}{3}$）-1=-2．

    查看答案和解析>>

    同步练习册答案